题目内容
1. 如图所示,点A,B,C,D在同一直线上,AB=CD,∠D=∠ECA,EC=FD,求证:AE=BF.
如图所示,点A,B,C,D在同一直线上,AB=CD,∠D=∠ECA,EC=FD,求证:AE=BF.
分析 根据等式的性质得出AC=BD,再利用SAS证明△AEC与△BFD全等,利用全等三角形的性质可得.
解答 证明:∵AB=CD,
∴AB+BC=CD+BC,
即AC=BD,
在△AEC与△BFD中,
$\left\{\begin{array}{l}{AC=BD}\\{∠D=∠ECA}\\{EC=FD}\end{array}\right.$,
∴△AEC≌△BFD(SAS),
∴AE=BF.
点评 此题考查全等三角形的判定和性质,关键是根据等式的性质得出AC=BD,再利用SAS证明△AEC与△BFD全等.

练习册系列答案
相关题目
11.若关于x的不等式组$\left\{\begin{array}{l}{5-2x<1}\\{x-a≤0}\end{array}\right.$的整数解只有1个,则a的取值范围是( )
| A. | 2<a<3 | B. | 3≤a<4 | C. | 2<a≤3 | D. | 3<a≤4 |
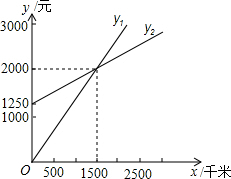 某单位准备租用一辆汽车,设汽车每月行驶x km,甲,乙两个出租车公司的月收费分别为y1元和y2元,y1,y2与x之间的函数关系图象如图,观察图象回答下列问题:
某单位准备租用一辆汽车,设汽车每月行驶x km,甲,乙两个出租车公司的月收费分别为y1元和y2元,y1,y2与x之间的函数关系图象如图,观察图象回答下列问题: 如图,在△ABC中,点D在边AB上,满足∠ACD=∠ABC,则△ADC∽△ACB,若AC=2,AD=1,则DB=3.
如图,在△ABC中,点D在边AB上,满足∠ACD=∠ABC,则△ADC∽△ACB,若AC=2,AD=1,则DB=3. 如图所示,已知AB⊥FC于B,DE⊥FC于E,AB,DF交于M,AC,DE交于N,BF=CE,AC=DF.求证:∠A=∠D.
如图所示,已知AB⊥FC于B,DE⊥FC于E,AB,DF交于M,AC,DE交于N,BF=CE,AC=DF.求证:∠A=∠D.
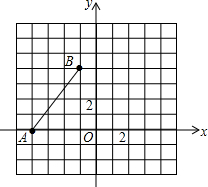 如图,已知A(-4,0),B(-1,4),将线段AB绕点O,顺时针旋转90°,得到线段A′B′.
如图,已知A(-4,0),B(-1,4),将线段AB绕点O,顺时针旋转90°,得到线段A′B′.