题目内容
11.已知a、b、c都是正整数,且满足条件:a2-b2-c2=abc,a2=2(b+c),求a-b-c的值.分析 根据a2-b2-c2=abc得到abc-a2+b2+c2=0,根据a2=2(b+c)=2b+2c得到abc-2b-2c+b2+c2=0,从而得到abc+(b-1)2+(c-1)2=0,进而求得b=1,c=1,a=2,最后确定答案即可.
解答 解:∵a2-b2-c2=abc,
∴abc-a2+b2+c2=0,
∵a2=2(b+c)=2b+2c,
∴abc-2b-2c+b2+c2=0,
∴abc+(b-1)2+(c-1)2=0,
∵a、b、c都是正整数,
∴abc≠1,
∴abc=2,
∴(b-1)2=0,(c-1)2=0,
∴b=1,c=1,a=2,
∴a-b-c=0.
点评 考查了因式分解的知识,解题的关键是能够对题目的已知条件进行变形,难度不是很大.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
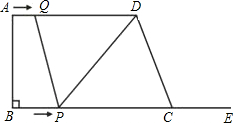 如图,在梯形ABCD中,AD∥BC,∠B=90°,AD=16cm,AB=12cm,BC=21cm,动点P从点B出发,沿射线BC的方向以每秒2cm的速度运动,动点Q从点A出发,在线段AD上以每秒1cm的速度向点D运动,点P,Q分别从点B,A同时出发,当点Q运动到点D时,点P随之停止运动,设运动的时间为t(秒).
如图,在梯形ABCD中,AD∥BC,∠B=90°,AD=16cm,AB=12cm,BC=21cm,动点P从点B出发,沿射线BC的方向以每秒2cm的速度运动,动点Q从点A出发,在线段AD上以每秒1cm的速度向点D运动,点P,Q分别从点B,A同时出发,当点Q运动到点D时,点P随之停止运动,设运动的时间为t(秒).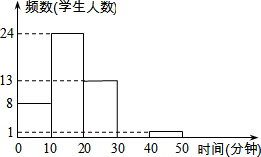 李老师为了解班里学生的作息时间,调查了班上50名学生上学路上花费的时间,他发现学生所花时间都少于50分钟,然后将调查数据整理,作出如下频数分布直方图的一部分(每组数据含最小值不含最大值).请根据该频数分布直方图,回答下列问题:
李老师为了解班里学生的作息时间,调查了班上50名学生上学路上花费的时间,他发现学生所花时间都少于50分钟,然后将调查数据整理,作出如下频数分布直方图的一部分(每组数据含最小值不含最大值).请根据该频数分布直方图,回答下列问题: 如图所示,已知AB⊥FC于B,DE⊥FC于E,AB,DF交于M,AC,DE交于N,BF=CE,AC=DF.求证:∠A=∠D.
如图所示,已知AB⊥FC于B,DE⊥FC于E,AB,DF交于M,AC,DE交于N,BF=CE,AC=DF.求证:∠A=∠D.