题目内容
20.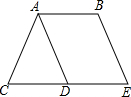 在平行四边形ABED中,CD为DE延长线,连接AC,AD恰好为∠BAC角平分线,且∠BAD=60°,BE=2cm,求△ACD的周长.
在平行四边形ABED中,CD为DE延长线,连接AC,AD恰好为∠BAC角平分线,且∠BAD=60°,BE=2cm,求△ACD的周长.
分析 首先证明AC=CD,再根据∠BAD=60°可得△ACD是等边三角形,进而可得AC=CD=AD,再根据平行四边形的性质可得AD=BE=2cm,进而可得答案.
解答 解:∵AD为∠BAC角平分线,
∴∠BAD=∠CAD,
∵四边形ABED是平行四边形,
∴AB∥DE,AD=EB=2cm,
∴∠BAD=∠ADC,
∴∠CAD=∠CDA,
∴AC=CD,
∵∠BAD=60°,
∴△ACD是等边三角形,
∴AC=CD=AD=2cm,
∴△ACD的周长为6cm.
点评 此题主要考查了平行四边形的性质,以及等边三角形的判定和性质,关键是掌握有一个角等于60°的等腰三角形是等边三角形.

练习册系列答案
相关题目
10.P是∠B的角平分线和∠C的角平分线在△ABC内的交点,∠BPC=120°,则∠A=( )
| A. | 30° | B. | 45° | C. | 60° | D. | 70° |
8.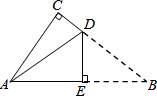 如图是一张直角三角形的纸片,两直角边AC=6cm、BC=8cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( )
如图是一张直角三角形的纸片,两直角边AC=6cm、BC=8cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( )
 如图是一张直角三角形的纸片,两直角边AC=6cm、BC=8cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( )
如图是一张直角三角形的纸片,两直角边AC=6cm、BC=8cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( )| A. | 4cm | B. | 5cm | C. | 6cm | D. | 10cm |
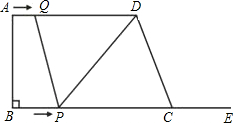 如图,在梯形ABCD中,AD∥BC,∠B=90°,AD=16cm,AB=12cm,BC=21cm,动点P从点B出发,沿射线BC的方向以每秒2cm的速度运动,动点Q从点A出发,在线段AD上以每秒1cm的速度向点D运动,点P,Q分别从点B,A同时出发,当点Q运动到点D时,点P随之停止运动,设运动的时间为t(秒).
如图,在梯形ABCD中,AD∥BC,∠B=90°,AD=16cm,AB=12cm,BC=21cm,动点P从点B出发,沿射线BC的方向以每秒2cm的速度运动,动点Q从点A出发,在线段AD上以每秒1cm的速度向点D运动,点P,Q分别从点B,A同时出发,当点Q运动到点D时,点P随之停止运动,设运动的时间为t(秒).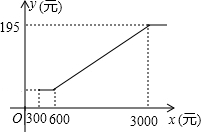 如图所示是我市企业职工养老保险个人月缴费y(元)随个人工资x(元)变化的图象,请你根据图象回答下面的问题:
如图所示是我市企业职工养老保险个人月缴费y(元)随个人工资x(元)变化的图象,请你根据图象回答下面的问题: 如图所示,已知AB⊥FC于B,DE⊥FC于E,AB,DF交于M,AC,DE交于N,BF=CE,AC=DF.求证:∠A=∠D.
如图所示,已知AB⊥FC于B,DE⊥FC于E,AB,DF交于M,AC,DE交于N,BF=CE,AC=DF.求证:∠A=∠D.