题目内容
9.甲计划用若干个工作日完成某项工作,从第二个工作日起,乙加入此项工作,且甲、乙两人工效相同,结果提前3天完成任务,则甲计划完成此项工作的天数是( )| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
分析 设甲计划完成此项工作的天数为x,根据甲先干一天后甲乙合作完成比甲单独完成提前3天即可得出关于x的一元一次方程,解之即可得出结论.
解答 解:设甲计划完成此项工作的天数为x,
根据题意得:x-(1+$\frac{x-1}{2}$)=3,
解得:x=7.
故选B.
点评 本题考查了一元一次方程的应用,根据甲先干一天后甲乙合作完成比甲单独完成提前3天列出关于x的一元一次方程是解题的关键.

练习册系列答案
相关题目
20.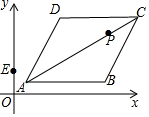 已知菱形ABCD在平面直角坐标系的位置如图所示,A(1,1),B(6,1),AC=4$\sqrt{5}$,点P是对角线OAC上的一个动点,E(0,2),当△EPD周长最小时,点P的坐标为( )
已知菱形ABCD在平面直角坐标系的位置如图所示,A(1,1),B(6,1),AC=4$\sqrt{5}$,点P是对角线OAC上的一个动点,E(0,2),当△EPD周长最小时,点P的坐标为( )
 已知菱形ABCD在平面直角坐标系的位置如图所示,A(1,1),B(6,1),AC=4$\sqrt{5}$,点P是对角线OAC上的一个动点,E(0,2),当△EPD周长最小时,点P的坐标为( )
已知菱形ABCD在平面直角坐标系的位置如图所示,A(1,1),B(6,1),AC=4$\sqrt{5}$,点P是对角线OAC上的一个动点,E(0,2),当△EPD周长最小时,点P的坐标为( )| A. | (2,2) | B. | (2,$\frac{11}{2}$) | C. | ($\frac{10}{7}$,$\frac{5}{7}$) | D. | ($\frac{9}{4}$,$\frac{13}{8}$) |
17.计算(-3)×2的结果是( )
| A. | 5 | B. | -5 | C. | 6 | D. | -6 |
4.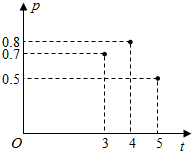 加工爆米花时,爆开且不糊的粒数占加工总粒数的百分比称为“可食用率”,在特定条件下,可食用率p与加工时间t(单位:分钟)满足函数关系p=at2+bt-2(a,b是常数),如图记录了三次实验的数据,根据上述函数模型和实验数据,可得到最佳加工时间为( )
加工爆米花时,爆开且不糊的粒数占加工总粒数的百分比称为“可食用率”,在特定条件下,可食用率p与加工时间t(单位:分钟)满足函数关系p=at2+bt-2(a,b是常数),如图记录了三次实验的数据,根据上述函数模型和实验数据,可得到最佳加工时间为( )
 加工爆米花时,爆开且不糊的粒数占加工总粒数的百分比称为“可食用率”,在特定条件下,可食用率p与加工时间t(单位:分钟)满足函数关系p=at2+bt-2(a,b是常数),如图记录了三次实验的数据,根据上述函数模型和实验数据,可得到最佳加工时间为( )
加工爆米花时,爆开且不糊的粒数占加工总粒数的百分比称为“可食用率”,在特定条件下,可食用率p与加工时间t(单位:分钟)满足函数关系p=at2+bt-2(a,b是常数),如图记录了三次实验的数据,根据上述函数模型和实验数据,可得到最佳加工时间为( )| A. | 3.75分钟 | B. | 4.00分钟 | C. | 4.15分钟 | D. | 4.25分钟 |
18.化简:$\frac{x-4}{{x}^{2}-9}$÷(1-$\frac{1}{x-3}$)的结果是( )
| A. | x-4 | B. | x+3 | C. | $\frac{1}{x-3}$ | D. | $\frac{1}{x+3}$ |
19. 已知实数m、n在数轴上的对应点的位置如图,则|m-n|+$\sqrt{1-2n+{n}^{2}}$=( )
已知实数m、n在数轴上的对应点的位置如图,则|m-n|+$\sqrt{1-2n+{n}^{2}}$=( )
 已知实数m、n在数轴上的对应点的位置如图,则|m-n|+$\sqrt{1-2n+{n}^{2}}$=( )
已知实数m、n在数轴上的对应点的位置如图,则|m-n|+$\sqrt{1-2n+{n}^{2}}$=( )| A. | m-1 | B. | m+1 | C. | 2n-m+1 | D. | 2n-m-1 |
 如图,AB是⊙O的切线,半径OA=2,OB交⊙O于C,∠B=30°,则阴影部分的面积为2$\sqrt{3}$-$\frac{1}{3}$π.(结果保留π)
如图,AB是⊙O的切线,半径OA=2,OB交⊙O于C,∠B=30°,则阴影部分的面积为2$\sqrt{3}$-$\frac{1}{3}$π.(结果保留π)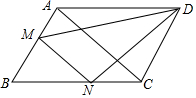 如图,在平行四边形ABCD中,MN∥AC,求证:S△ADM=S△CDN.
如图,在平行四边形ABCD中,MN∥AC,求证:S△ADM=S△CDN.