题目内容
19. 如图,AB是⊙O的切线,半径OA=2,OB交⊙O于C,∠B=30°,则阴影部分的面积为2$\sqrt{3}$-$\frac{1}{3}$π.(结果保留π)
如图,AB是⊙O的切线,半径OA=2,OB交⊙O于C,∠B=30°,则阴影部分的面积为2$\sqrt{3}$-$\frac{1}{3}$π.(结果保留π)
分析 根据阴影部分的面积=△OAB的面积-扇形AOC的面积计算即可.
解答 解:
∵AB是⊙O的切线,
∴OA⊥AB,
∵OA=2,∠B=30°,
∴OB=4,
∴AB=$\sqrt{O{B}^{2}-O{A}^{2}}$=2$\sqrt{3}$,∠O=60°,
∴阴影部分的面积=△OAB的面积-扇形AOC的面积=$\frac{1}{2}$×2×2$\sqrt{3}$-$\frac{30π×4}{360}$=2$\sqrt{3}$-$\frac{1}{3}$π,
故答案为:2$\sqrt{3}$-$\frac{1}{3}$π.
点评 本题考查的是切线的性质、扇形面积的计算,掌握切线的性质定理、扇形的面积公式是解题的关键.

练习册系列答案
相关题目
10.已知点P(a,2),Q(-1,b)关于x轴对称,则点(a,b)位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
7.如图,等腰Rt△ABC中,∠ACB=90°,AC=BC=1,且AC边在直线a上,将△ABC绕点A瞬时针旋转到位置①可得到点P1,此时AP1=$\sqrt{2}$;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=$\sqrt{2}$+1;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=$\sqrt{2}$+2;…,按此规律继续旋转,直至得到点P2017为止,则AP2017长为( )


| A. | 1344+672$\sqrt{2}$ | B. | 1344+673$\sqrt{2}$ | C. | 1345+673$\sqrt{2}$ | D. | 1345+674$\sqrt{2}$ |
14.在Rt△ABC中,∠C=90°,AB=6,cosB=$\frac{2}{3}$,则BC的长为( )
| A. | $\sqrt{5}$ | B. | 4 | C. | 2$\sqrt{5}$ | D. | 5 |
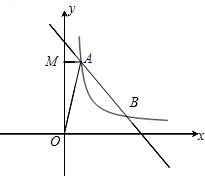 如图,一次函数y=mx+5的图象与反比例函数$y=\frac{k}{x}$(k≠0)在第一象限的图象交于A(1,n)和B(4,1)两点,过点A作y轴的垂线,垂足为M,
如图,一次函数y=mx+5的图象与反比例函数$y=\frac{k}{x}$(k≠0)在第一象限的图象交于A(1,n)和B(4,1)两点,过点A作y轴的垂线,垂足为M,