题目内容
4.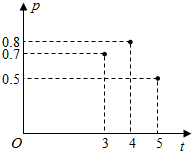 加工爆米花时,爆开且不糊的粒数占加工总粒数的百分比称为“可食用率”,在特定条件下,可食用率p与加工时间t(单位:分钟)满足函数关系p=at2+bt-2(a,b是常数),如图记录了三次实验的数据,根据上述函数模型和实验数据,可得到最佳加工时间为( )
加工爆米花时,爆开且不糊的粒数占加工总粒数的百分比称为“可食用率”,在特定条件下,可食用率p与加工时间t(单位:分钟)满足函数关系p=at2+bt-2(a,b是常数),如图记录了三次实验的数据,根据上述函数模型和实验数据,可得到最佳加工时间为( )| A. | 3.75分钟 | B. | 4.00分钟 | C. | 4.15分钟 | D. | 4.25分钟 |
分析 根据题目数据求出函数解析式,根据二次函数的性质可得.
解答 解:根据题意,将(3,0.7)、(4,0.8)、(5,0.5)代入p=at2+bt+c,
得:
$\left\{\begin{array}{l}{9a+3b+c=0.7}\\{16a+4b+c=0.8}\\{25a+5b+c=0.5}\end{array}\right.$,
解得:
$\left\{\begin{array}{l}{a=-0.2}\\{b=1.5}\\{c=-2}\end{array}\right.$,
即p=-0.2t2+1.5t-2,
当t=-$\frac{1.5}{-0.2×2}$=3.75时,p取得最大值,
故选:A.
点评 本题主要考查二次函数的应用,利用二次函数的图象和性质求最值问题是解题的关键.

练习册系列答案
相关题目
14.在Rt△ABC中,∠C=90°,AB=6,cosB=$\frac{2}{3}$,则BC的长为( )
| A. | $\sqrt{5}$ | B. | 4 | C. | 2$\sqrt{5}$ | D. | 5 |
15.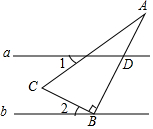 直线a∥b,直角三角形如图放置,若∠1+∠A=65°,则∠2的度数为( )
直线a∥b,直角三角形如图放置,若∠1+∠A=65°,则∠2的度数为( )
 直线a∥b,直角三角形如图放置,若∠1+∠A=65°,则∠2的度数为( )
直线a∥b,直角三角形如图放置,若∠1+∠A=65°,则∠2的度数为( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
12.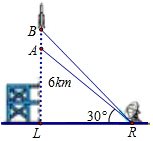 如图,一枚运载火箭从地面L处发射,当火箭到达A点时,从位于地面R处的雷达站观测得知AR的距离是6km,仰角∠ARL=30°,又经过1s后火箭到达B点,此时测得仰角∠BRL=45°,则这枚火箭从A到B的平均速度为( )km/s.
如图,一枚运载火箭从地面L处发射,当火箭到达A点时,从位于地面R处的雷达站观测得知AR的距离是6km,仰角∠ARL=30°,又经过1s后火箭到达B点,此时测得仰角∠BRL=45°,则这枚火箭从A到B的平均速度为( )km/s.
 如图,一枚运载火箭从地面L处发射,当火箭到达A点时,从位于地面R处的雷达站观测得知AR的距离是6km,仰角∠ARL=30°,又经过1s后火箭到达B点,此时测得仰角∠BRL=45°,则这枚火箭从A到B的平均速度为( )km/s.
如图,一枚运载火箭从地面L处发射,当火箭到达A点时,从位于地面R处的雷达站观测得知AR的距离是6km,仰角∠ARL=30°,又经过1s后火箭到达B点,此时测得仰角∠BRL=45°,则这枚火箭从A到B的平均速度为( )km/s.| A. | 3$\sqrt{3}$-3 | B. | 3$\sqrt{3}$ | C. | 3$\sqrt{3}$+3 | D. | 3 |
19.若a2-b2=-$\frac{1}{16}$,a+b=-$\frac{1}{4}$,则a-b的值为( )
| A. | $\frac{1}{4}$ | B. | -$\frac{1}{4}$ | C. | 2 | D. | 4 |
14. 如图,⊙O的半径为2,AB,CD是两条互相垂直的直径,点P是⊙O上任意一点(点P与点A,B,C,D均不重合),过点P作PM⊥AB于点M.PN⊥CD于点N,点Q是线段MN的中点.若点P以点O为旋转中心.沿着圆周顺时针旋转45°.则点Q经过的路径长为( )
如图,⊙O的半径为2,AB,CD是两条互相垂直的直径,点P是⊙O上任意一点(点P与点A,B,C,D均不重合),过点P作PM⊥AB于点M.PN⊥CD于点N,点Q是线段MN的中点.若点P以点O为旋转中心.沿着圆周顺时针旋转45°.则点Q经过的路径长为( )
 如图,⊙O的半径为2,AB,CD是两条互相垂直的直径,点P是⊙O上任意一点(点P与点A,B,C,D均不重合),过点P作PM⊥AB于点M.PN⊥CD于点N,点Q是线段MN的中点.若点P以点O为旋转中心.沿着圆周顺时针旋转45°.则点Q经过的路径长为( )
如图,⊙O的半径为2,AB,CD是两条互相垂直的直径,点P是⊙O上任意一点(点P与点A,B,C,D均不重合),过点P作PM⊥AB于点M.PN⊥CD于点N,点Q是线段MN的中点.若点P以点O为旋转中心.沿着圆周顺时针旋转45°.则点Q经过的路径长为( )| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{3}$ |