题目内容
19．
已知实数m、n在数轴上的对应点的位置如图，则|m-n|+$\sqrt{1-2n+{n}^{2}}$=（ ）| A． | m-1 | B． | m+1 | C． | 2n-m+1 | D． | 2n-m-1 |
分析 根据数轴上点的位置判断出m-n与n-1的正负，利用二次根式性质及绝对值的代数意义化简即可得到结果．
解答 解：根据数轴上点的位置得：m＜0＜1＜n，
∴m-n＜0，n-1＞0，
则原式=|m-n|+|n-1|=n-m+n-1=2n-m-1，
故选D
点评 此题考查了二次根式的性质与化简，以及实数与数轴，判断出各式的正负是解本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
7．如图，将正方形ABCD的四个角向内折起，恰好拼成一个无缝无重叠的四边形EFGH，再将四边形EFGH的一个角向内折起，使点F恰好和EG的中点重合，折痕为IJ，若点H到IJ的距离HK=9cm，则边AB的长是（ ）
| A． | 16cm | B． | 12cm | C． | 9cm | D． | 6$\sqrt{2}$cm |
14．
如图，⊙O的半径为2，AB，CD是两条互相垂直的直径，点P是⊙O上任意一点（点P与点A，B，C，D均不重合），过点P作PM⊥AB于点M．PN⊥CD于点N，点Q是线段MN的中点．若点P以点O为旋转中心．沿着圆周顺时针旋转45°．则点Q经过的路径长为（ ）
如图，⊙O的半径为2，AB，CD是两条互相垂直的直径，点P是⊙O上任意一点（点P与点A，B，C，D均不重合），过点P作PM⊥AB于点M．PN⊥CD于点N，点Q是线段MN的中点．若点P以点O为旋转中心．沿着圆周顺时针旋转45°．则点Q经过的路径长为（ ）| A． | $\frac{π}{4}$ | B． | $\frac{π}{2}$ | C． | $\frac{π}{6}$ | D． | $\frac{π}{3}$ |
10．
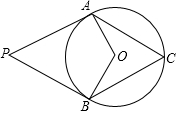如图，PA、PB是⊙O的两条切线，A、B为切点，C为优弧BA上一动点．若OA=15，sin∠C=$\frac{4}{5}$，则S△PAB的值为（ ）
如图，PA、PB是⊙O的两条切线，A、B为切点，C为优弧BA上一动点．若OA=15，sin∠C=$\frac{4}{5}$，则S△PAB的值为（ ）| A． | 108 | B． | 150 | C． | 300 | D． | 192 |