题目内容
20.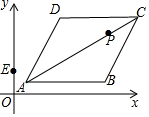 已知菱形ABCD在平面直角坐标系的位置如图所示,A(1,1),B(6,1),AC=4$\sqrt{5}$,点P是对角线OAC上的一个动点,E(0,2),当△EPD周长最小时,点P的坐标为( )
已知菱形ABCD在平面直角坐标系的位置如图所示,A(1,1),B(6,1),AC=4$\sqrt{5}$,点P是对角线OAC上的一个动点,E(0,2),当△EPD周长最小时,点P的坐标为( )| A. | (2,2) | B. | (2,$\frac{11}{2}$) | C. | ($\frac{10}{7}$,$\frac{5}{7}$) | D. | ($\frac{9}{4}$,$\frac{13}{8}$) |
分析 点D关于AC的对称点是点B,连接EB,交AC于点P,再得出EB即为EP+DP最短,解答即可.
解答 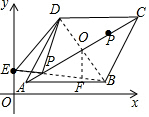 解:连接ED,如图,
解:连接ED,如图,
∵点D关于AC的对称点是点B,
∴DP=BP,
∴EB即为EP+DP最短,
即此时△EPD周长最小,
连接BD交AC于O,
过O作OF⊥AB于F,
∵四边形ABCD是菱形,
∴AO=$\frac{1}{2}$AC=2$\sqrt{5}$,AC⊥BD,
∴BO=$\sqrt{A{B}^{2}-A{O}^{2}}$=$\sqrt{5}$,
∴OF=$\frac{AO•OB}{AB}$=2,
∴AF=$\sqrt{A{O}^{2}-O{F}^{2}}$=4,
∵A(1,1),B(6,1),
∴AB∥x轴,
∴直线AB与x轴间的距离是1,
∴O点的纵坐标为2+1=3,
∴O(5,3),
∴直线AC的解析式为:y=$\frac{1}{2}$x+$\frac{1}{2}$,
∵E(0,2),B(6,1),
∴直线BE的解析式为:y=-$\frac{1}{6}$x+2,
解$\left\{\begin{array}{l}{y=-\frac{1}{6}x+2}\\{y=\frac{1}{2}x+\frac{1}{2}}\end{array}\right.$得:$\left\{\begin{array}{l}{x=\frac{9}{4}}\\{y=\frac{13}{8}}\end{array}\right.$,
∴P($\frac{9}{4}$,$\frac{13}{8}$).
故选D.
点评 此题考查了轴对称-最短距离问题,菱形的性质,关键是根据一次函数与方程组的关系,得出两直线的解析式,求出其交点坐标.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
10.已知点P(a,2),Q(-1,b)关于x轴对称,则点(a,b)位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
11.若方程组$\left\{\begin{array}{l}{x+y=a}\\{x-y=4a}\end{array}\right.$的解是二元一次方程3x-5y-90=0的一个解,则a的值是( )
| A. | 3 | B. | 2 | C. | 6 | D. | 7 |
15.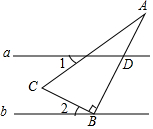 直线a∥b,直角三角形如图放置,若∠1+∠A=65°,则∠2的度数为( )
直线a∥b,直角三角形如图放置,若∠1+∠A=65°,则∠2的度数为( )
 直线a∥b,直角三角形如图放置,若∠1+∠A=65°,则∠2的度数为( )
直线a∥b,直角三角形如图放置,若∠1+∠A=65°,则∠2的度数为( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
5.蜀山区三月中旬每天平均空气质量指数(AQI)分别为:118,96,60,82,56,69,86,112,108,94,为了描述这十天空气质量的变化情况,最适合用的统计图是( )
| A. | 折线统计图 | B. | 频数分布直方图 | C. | 条形统计图 | D. | 扇形统计图 |
12.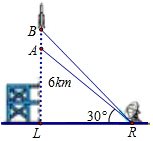 如图,一枚运载火箭从地面L处发射,当火箭到达A点时,从位于地面R处的雷达站观测得知AR的距离是6km,仰角∠ARL=30°,又经过1s后火箭到达B点,此时测得仰角∠BRL=45°,则这枚火箭从A到B的平均速度为( )km/s.
如图,一枚运载火箭从地面L处发射,当火箭到达A点时,从位于地面R处的雷达站观测得知AR的距离是6km,仰角∠ARL=30°,又经过1s后火箭到达B点,此时测得仰角∠BRL=45°,则这枚火箭从A到B的平均速度为( )km/s.
 如图,一枚运载火箭从地面L处发射,当火箭到达A点时,从位于地面R处的雷达站观测得知AR的距离是6km,仰角∠ARL=30°,又经过1s后火箭到达B点,此时测得仰角∠BRL=45°,则这枚火箭从A到B的平均速度为( )km/s.
如图,一枚运载火箭从地面L处发射,当火箭到达A点时,从位于地面R处的雷达站观测得知AR的距离是6km,仰角∠ARL=30°,又经过1s后火箭到达B点,此时测得仰角∠BRL=45°,则这枚火箭从A到B的平均速度为( )km/s.| A. | 3$\sqrt{3}$-3 | B. | 3$\sqrt{3}$ | C. | 3$\sqrt{3}$+3 | D. | 3 |