题目内容
1．
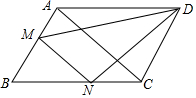如图，在平行四边形ABCD中，MN∥AC，求证：S△ADM=S△CDN．
分析 如图连接AN、CM．由AB∥CD，AD∥CB，推出S△AMD=S△AMC，S△NCD=S△NCA，由MN∥AC，推出S△ACM=S△ACN，由此即可证明．
解答 解：如图连接AN、CM．
∵四边形ABCD是平行四边形，
∴AB∥CD，AD∥CB，
∴S△AMD=S△AMC，S△NCD=S△NCA，
∵MN∥AC，
∴S△ACM=S△ACN，
∴S△ADM=S△CDN．
点评 本题考查平行四边形的性质，解题的关键是掌握同底等高的三角形的面积相等，属于中考常考题型．
练习册系列答案
阅读快车系列答案
相关题目
11．若方程组$\left\{\begin{array}{l}{x+y=a}\\{x-y=4a}\end{array}\right.$的解是二元一次方程3x-5y-90=0的一个解，则a的值是（ ）
| A． | 3 | B． | 2 | C． | 6 | D． | 7 |
12．
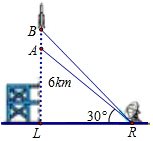如图，一枚运载火箭从地面L处发射，当火箭到达A点时，从位于地面R处的雷达站观测得知AR的距离是6km，仰角∠ARL=30°，又经过1s后火箭到达B点，此时测得仰角∠BRL=45°，则这枚火箭从A到B的平均速度为（ ）km/s．
如图，一枚运载火箭从地面L处发射，当火箭到达A点时，从位于地面R处的雷达站观测得知AR的距离是6km，仰角∠ARL=30°，又经过1s后火箭到达B点，此时测得仰角∠BRL=45°，则这枚火箭从A到B的平均速度为（ ）km/s．| A． | 3$\sqrt{3}$-3 | B． | 3$\sqrt{3}$ | C． | 3$\sqrt{3}$+3 | D． | 3 |
6．
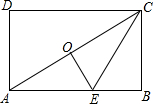如图，已知矩形ABCD中，点E在AB上，点O是对角线AC的中点，沿CE折叠后，点B恰好与点O重合，若BC=6，则折痕CE的长为（ ）
如图，已知矩形ABCD中，点E在AB上，点O是对角线AC的中点，沿CE折叠后，点B恰好与点O重合，若BC=6，则折痕CE的长为（ ）| A． | 2$\sqrt{3}$ | B． | 4$\sqrt{3}$ | C． | 8 | D． | 10 |