题目内容
14.已知关于x的一元二次方程方程(a-2)x2+2ax+a-3=0.(1)若方程有两个实数根,求a的取值范围.
(2)若x1,x2是方程的两个实数根,且${{x}_{1}}^{2}$x2+x1${{x}_{2}}^{2}$=-1,试求a的值.
分析 (1)根据根的判别式和已知得出a-2≠0且△≥0,求出即可;
(2)根据根与系数的关系得出x1+x2=-$\frac{2a}{a-2}$,x1•x2=$\frac{a-3}{a-2}$,变形后代入,即可得出关于a的方程,求出方程的解即可.
解答 解:(1)∵关于x的一元二次方程方程(a-2)x2+2ax+a-3=0有两个实数根,
∴a-2≠0且△≥0,
即a≠2,
△=(2a)2-4(a-2)(a-3)=20a-24≥0,
a≥$\frac{6}{5}$,
即a的取值范围是a≥$\frac{6}{5}$且a≠2;
(2)根据根与系数的关系得:x1+x2=-$\frac{2a}{a-2}$,x1•x2=$\frac{a-3}{a-2}$,
∵${{x}_{1}}^{2}$x2+x1${{x}_{2}}^{2}$=-1,
∴x1x2(x1+x2)=-1,
∴$\frac{a-3}{a-2}$•(-$\frac{2a}{a-2}$)=-1,
解得:a=1$±\sqrt{5}$,
由(1)知:a≥$\frac{6}{5}$且a≠2,
∴a=1-$\sqrt{5}$舍去,
所以a=1+$\sqrt{5}$.
点评 本题考查了根的判别式和根与系数的关系等知识点,能熟记根与系数的关系和根的判别式的内容是解此题的关键.

练习册系列答案
相关题目
5.蜀山区三月中旬每天平均空气质量指数(AQI)分别为:118,96,60,82,56,69,86,112,108,94,为了描述这十天空气质量的变化情况,最适合用的统计图是( )
| A. | 折线统计图 | B. | 频数分布直方图 | C. | 条形统计图 | D. | 扇形统计图 |
2.小明拿来n个形状大小完全相同的正方体木块,整齐地摆放在桌上,其三视图如图所示,则n的值是( )


| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
6.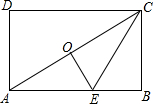 如图,已知矩形ABCD中,点E在AB上,点O是对角线AC的中点,沿CE折叠后,点B恰好与点O重合,若BC=6,则折痕CE的长为( )
如图,已知矩形ABCD中,点E在AB上,点O是对角线AC的中点,沿CE折叠后,点B恰好与点O重合,若BC=6,则折痕CE的长为( )
 如图,已知矩形ABCD中,点E在AB上,点O是对角线AC的中点,沿CE折叠后,点B恰好与点O重合,若BC=6,则折痕CE的长为( )
如图,已知矩形ABCD中,点E在AB上,点O是对角线AC的中点,沿CE折叠后,点B恰好与点O重合,若BC=6,则折痕CE的长为( )| A. | 2$\sqrt{3}$ | B. | 4$\sqrt{3}$ | C. | 8 | D. | 10 |
3.下列图形中既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
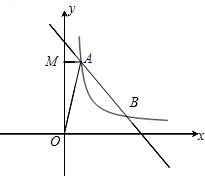 如图,一次函数y=mx+5的图象与反比例函数$y=\frac{k}{x}$(k≠0)在第一象限的图象交于A(1,n)和B(4,1)两点,过点A作y轴的垂线,垂足为M,
如图,一次函数y=mx+5的图象与反比例函数$y=\frac{k}{x}$(k≠0)在第一象限的图象交于A(1,n)和B(4,1)两点,过点A作y轴的垂线,垂足为M, E、F在菱形ABCD的边AB和BC上,DE=DF=AD,且∠EDF=30°,则∠BEF=35°.
E、F在菱形ABCD的边AB和BC上,DE=DF=AD,且∠EDF=30°,则∠BEF=35°.