题目内容
9.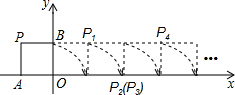 如图,将边长为1的正方形OPAB沿x轴正方向连续翻转2015次,点P依次落在点P1,P2,P3,…,P2014,P2015的位置,记Pi(xi,yi),i=1,2,3,…,2014,2015,则P2015的横坐标为2014.
如图,将边长为1的正方形OPAB沿x轴正方向连续翻转2015次,点P依次落在点P1,P2,P3,…,P2014,P2015的位置,记Pi(xi,yi),i=1,2,3,…,2014,2015,则P2015的横坐标为2014.
分析 观察规律可知纵坐标每4个一循环,可以判断P2015在503次循环后与P3纵坐标一致,以此可以求出P2015的横坐标,利用xn=xn+1时,则下一个点横坐标减1进而得出答案.
解答 解:根据规律:
P1(1,1),P2(2,0)=P3,P4(3,1)
P5(5,1),P6(6,0)=P7,P8(7,1)…
每4个一循环,2015÷4=503…3;
可以判断P2015在503次循环后与P3纵坐标一致,坐标应该是(2014,0);
故答案为:2014.
点评 本题考查了点的坐标的规律变化,根据正方形的性质,判断出每翻转4次为一个循环组是解题的关键,要注意翻转一个循环组点P向右前行4个单位.

练习册系列答案
相关题目
1.如图,从边长为a+2的正方形纸片中剪去一个边长为a-1的正方形(a>1),剩余部分沿虚线剪开,再拼成一个长方形(不重叠无缝隙),则该长方形的面积是( )
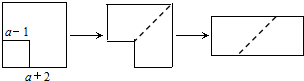

| A. | 4a+1 | B. | 4a+3 | C. | 6a+3 | D. | a2+1 |
18.某班52名师生准备全部去亮子河旅游,为确定旅游费用,班主任刘老师派班长去了解船只租金情况,班长得到如下表格:
(1)若单租A型船或B型船,至少需多少只?
(2)如果两种船都租,且既不超载也不空载,那么你能设计出几种租船方案?
(3)若你是班长,使总租金最少,应该选择怎样的租船方案?
| A型 | B型 | |
| (人/只) | 5 | 3 |
| (元/只) | 160 | 105 |
(2)如果两种船都租,且既不超载也不空载,那么你能设计出几种租船方案?
(3)若你是班长,使总租金最少,应该选择怎样的租船方案?
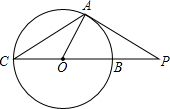 如图,已知CB是⊙O的直径,点A在圆上,且∠AOB=60°,连接OA,过点A作PA⊥OA交CB的延长线于点P,PA=4$\sqrt{3}$.
如图,已知CB是⊙O的直径,点A在圆上,且∠AOB=60°,连接OA,过点A作PA⊥OA交CB的延长线于点P,PA=4$\sqrt{3}$.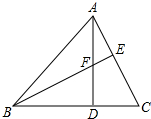 如图,已知AD是△ABC的高,F是AD上一点,BF的延长线交AC于点E,BF=AC,DF=DC,则BF与AC垂直吗?为什么?
如图,已知AD是△ABC的高,F是AD上一点,BF的延长线交AC于点E,BF=AC,DF=DC,则BF与AC垂直吗?为什么?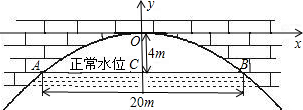 有座抛物线形拱桥(如图),正常水位时桥下河面宽20m,河面距拱顶4m,为了保证过往船只顺利航行,桥下水面的宽度不得小于18m.
有座抛物线形拱桥(如图),正常水位时桥下河面宽20m,河面距拱顶4m,为了保证过往船只顺利航行,桥下水面的宽度不得小于18m.