题目内容
12.已知抛物线y=(k+1)x2-2(k-2)x+2k+4与x轴的两交点一个在(2,0)左边,另一个在(2,0)右边,则k的取值范围是-8<k<-1.分析 若k+1>0时,抛物线开口向上,则x=2时,对应的函数值<0,若k+1<0时,抛物线开口向下,则x=2时,对应的函数值>0,从而可解的k的取值范围.
解答 解:当k+1>0时,抛物线开口向上,
∵抛物线y=(k+1)x2-2(k-2)x+2k+4与x轴的两交点一个在(2,0)左边,另一个在(2,0)右边,
∴当x=2时,y<0,即4(k+1)-4(k-2)+2k+4<0①且k+1>0②.
解不等式①得:k<-8,解不等式②得k>-1.
所以不等式组无解.
当k+1<0时,抛物线开口向下,
∵抛物线y=(k+1)x2-2(k-2)x+2k+4与x轴的两交点一个在(2,0)左边,另一个在(2,0)右边,
∴4(k+1)-4(k-2)+2k+4<0①且k+1<0②.
解不等式①得:k>-8,解不等式②得k<-1.
∴-8<k<-1.
故答案为:-8<k<-1.
点评 本题主要考查的是抛物线与x轴的交点,根据二次函数的性质列出关于k的不等式组是解题的关键.

练习册系列答案
相关题目
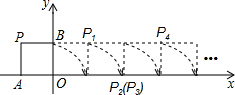 如图,将边长为1的正方形OPAB沿x轴正方向连续翻转2015次,点P依次落在点P1,P2,P3,…,P2014,P2015的位置,记Pi(xi,yi),i=1,2,3,…,2014,2015,则P2015的横坐标为2014.
如图,将边长为1的正方形OPAB沿x轴正方向连续翻转2015次,点P依次落在点P1,P2,P3,…,P2014,P2015的位置,记Pi(xi,yi),i=1,2,3,…,2014,2015,则P2015的横坐标为2014. 某包装公司想用一张不规则的包装纸做一个正方体纸盒,如图.
某包装公司想用一张不规则的包装纸做一个正方体纸盒,如图. 如图,D为△ABC的边BC的中点,F为AC边上的点,AF=$\frac{1}{2}$FC,BF交AD于点E.求证:点E为AD的中点.
如图,D为△ABC的边BC的中点,F为AC边上的点,AF=$\frac{1}{2}$FC,BF交AD于点E.求证:点E为AD的中点. 如图,在△ABC中,AB=AC,延长AB到D,使BD=AB,E为AB的中点,连结CE、CD,求证:
如图,在△ABC中,AB=AC,延长AB到D,使BD=AB,E为AB的中点,连结CE、CD,求证: 如图,矩形ABCD中,对角线AC,BD交于点O,AB=6,BC=8.动点P从点B出发沿BC以每秒1个单位长度的速度向点C匀速运动,同时动点Q从点C出发沿CD方向,方向,以每秒1个单位长度的速度向点C匀速运动,同时动点Q从点C出发沿CD方向,以每秒1个单位长度的速度向点D匀速运动,当其中一个点到达终点后即都停止运动,过点Q作QM∥AC交AD于点M,连接PM,PQ,设点P的运动时间为t秒,△PQM的面积为S.
如图,矩形ABCD中,对角线AC,BD交于点O,AB=6,BC=8.动点P从点B出发沿BC以每秒1个单位长度的速度向点C匀速运动,同时动点Q从点C出发沿CD方向,方向,以每秒1个单位长度的速度向点C匀速运动,同时动点Q从点C出发沿CD方向,以每秒1个单位长度的速度向点D匀速运动,当其中一个点到达终点后即都停止运动,过点Q作QM∥AC交AD于点M,连接PM,PQ,设点P的运动时间为t秒,△PQM的面积为S. 已知,如图,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,且∠A=90°.求证:△BCD是直角三角形.
已知,如图,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,且∠A=90°.求证:△BCD是直角三角形.