题目内容
15. 已知一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于A(2,2),B(-1,m)
已知一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于A(2,2),B(-1,m)(1)求一次函数和反比例函数的解析式;
(2)在给定的直角坐标系中,画出这两个函数的图象;
(3)当x为何值时,一次函数的值大于反比例函数的值?
分析 (1)由点A在反比例函数图象上结合反比例函数系数k的几何意义可得出k的值,从而得出反比例函数解析式;将x=-1代入到反比例函数解析式中,求出m的值,即找出点B的坐标,由A、B两点的坐标利用待定系数法即可求出一次函数解析式;
(2)由A、B两点可直接画出一次函数图象,结合反比例函数的对称性即可画出反比例函数图象;
(3)结合函数图象,寻找一次函数图象在反比例函数图象上方时,x的取值范围.
解答 解:(1)∵点A(2,2)为反比例函数图象上一点,
∴k=2×2=4,
反比例函数解析式为y=$\frac{4}{x}$.
令x=-1,则m=y=$\frac{4}{-1}$=-4,
∴点B的坐标为(-1,-4).
将点A(2,2)、点B(-1,-4)代入到一次函数y=ax+b中,
$\left\{\begin{array}{l}{2=2a+b}\\{-4=-a+b}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=2}\\{b=-2}\end{array}\right.$.
∴一次函数的解析式为y=2x-2.
(2)在直角坐标系中,找出A、B两点,过该两点画出直线AB以及反比例函数y=$\frac{4}{x}$的图象,如图所示.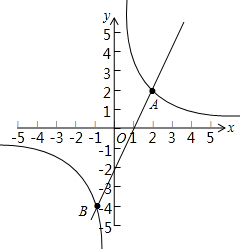
(3)结合两函数的图象可知:2x-2>$\frac{4}{x}$时,-1<x<0或2<x.
故当-1<x<0或2<x时,一次函数的值大于反比例函数的值.
点评 本题考查了反比例函数与一次函数的交点问题、待定系数法求函数解析式以及利用函数图象解不等式,解题的关键是:(1)求出点B的坐标;(2)画出两个函数图象;(3)结合函数图象解不等式.本题属于基础题,难度不大,解决该题型题目时,利用待定系数法求出函数解析式是关键.

 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案| A. | $\frac{1}{3}$ | B. | $\frac{4}{9}$ | C. | $\frac{2}{9}$ | D. | $\frac{2}{3}$ |
| A. | 没有实数根 | B. | 有一个实数根 | C. | 有两个实数根 | D. | 有三个实数根 |
①线段a垂直于投影面P,则线段a在投影面P上的正投影是一个点;②长方形的对角线垂直于投影面,则长方形在投影面上的正投影是一条线段;③正方体的一侧面与投影面平行,则该正方体有4个面的正投影是线段;④圆锥的轴截面与投影面平行,则圆锥在投影面上的正投影是等腰三角形.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | 20cm2 | B. | 300cm2 | C. | 400cm2 | D. | 600cm2 |
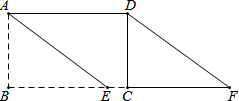 如图,矩形ABCD中,AD=5,AB=3,在BC边上取一点E,使BE=4,连结AE,沿AE剪下△ABE,将它平移至△DCF的位置,拼成四边形AEFD.
如图,矩形ABCD中,AD=5,AB=3,在BC边上取一点E,使BE=4,连结AE,沿AE剪下△ABE,将它平移至△DCF的位置,拼成四边形AEFD.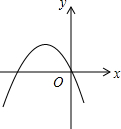 二次函数y=ax2+bx+c的图象如图,解不等式bx+a>0.
二次函数y=ax2+bx+c的图象如图,解不等式bx+a>0.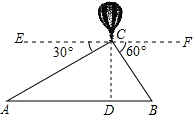 如图所示,从热气球C上测定建筑物A、B底部的俯角分别为30°和60°,已知AB间的距离为180米,CD垂直于AB于点D.问:此时热气球的高度为多少?
如图所示,从热气球C上测定建筑物A、B底部的俯角分别为30°和60°,已知AB间的距离为180米,CD垂直于AB于点D.问:此时热气球的高度为多少?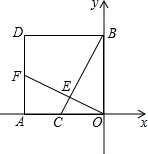 如图,边长为4的正方形OADB的边OA、OB分别在x轴、y轴上,点C为OA的中点,OF⊥BC于E,交AD于F.
如图,边长为4的正方形OADB的边OA、OB分别在x轴、y轴上,点C为OA的中点,OF⊥BC于E,交AD于F.