题目内容
5.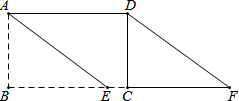 如图,矩形ABCD中,AD=5,AB=3,在BC边上取一点E,使BE=4,连结AE,沿AE剪下△ABE,将它平移至△DCF的位置,拼成四边形AEFD.
如图,矩形ABCD中,AD=5,AB=3,在BC边上取一点E,使BE=4,连结AE,沿AE剪下△ABE,将它平移至△DCF的位置,拼成四边形AEFD.(1)求证:四边形AEFD是菱形;
(2)求四边形AEFD的两条对角线的长.
分析 (1)根据平移的性质得到AE∥DF,AE=DF,则由此判定四边形AEFD是平行四边形;然后由“邻边相等的平行四边形是菱形”证得结论;
(2)根据勾股定理,可得答案.
解答 (1)证明:由平移的性质得:AE∥DF,AE=DF,
∴四边形AEFD是平行四边形.
∵四边形ABCD是矩形,
∴∠B=∠DCE=90°,
∴AE=$\sqrt{A{B}^{2}+B{E}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5=AD,
∴四边形AEFD是菱形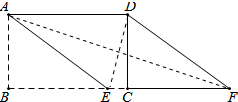
(2)解:连结DE、AF,如图所示:
在直角△ABF中,BF=BE+EF=4+5=9,
由勾股定理得到:AF=$\sqrt{A{B}^{2}{+BF}^{2}}$=$\sqrt{{3}^{2}+{9}^{2}}$=3$\sqrt{10}$,
在直角△DCE中,CE=BC-BE=5-4=1,
由勾股定理得到:DE=$\sqrt{C{D}^{2}+C{E}^{2}}$=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$.
点评 本题考查了菱形的判定与性质、图形的剪拼以及平移的性质、勾股定理.熟练掌握菱形的判定与性质,由勾股定理得出AE是解决问题的关键.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
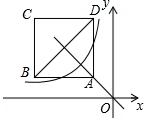 如图,正方形ABCD位于第二象限,边长为2,点A在直线y=-x上,点A的横坐标为-1,正方形ABCD的边分别平行于x轴、y轴.若双曲线y=$\frac{k}{x}$与正方形ABCD有公共点,则k的取值范围为-9≤k≤-1.
如图,正方形ABCD位于第二象限,边长为2,点A在直线y=-x上,点A的横坐标为-1,正方形ABCD的边分别平行于x轴、y轴.若双曲线y=$\frac{k}{x}$与正方形ABCD有公共点,则k的取值范围为-9≤k≤-1.
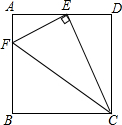 如图,在正方形ABCD中,点E为AD的中点,连接EC,过点E作EF⊥EC,交AB于点F,则tan∠ECF=$\frac{1}{2}$.
如图,在正方形ABCD中,点E为AD的中点,连接EC,过点E作EF⊥EC,交AB于点F,则tan∠ECF=$\frac{1}{2}$. 已知:如图,⊙O的半径OC垂直弦AB于点H,连接BC,过点A作弦AE∥BC,过点C作CD∥BA交EA延长线于点D,延长CO交AE于点F.
已知:如图,⊙O的半径OC垂直弦AB于点H,连接BC,过点A作弦AE∥BC,过点C作CD∥BA交EA延长线于点D,延长CO交AE于点F. 已知一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于A(2,2),B(-1,m)
已知一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于A(2,2),B(-1,m)