题目内容
3.已知b=$\frac{\sqrt{{a}^{2}-4}-3\sqrt{4-{a}^{2}}}{a-2}$+b,求值:(1)ba; (2)(a+b)2015.分析 先根据二次根式及分式有意义的条件求出a的值,求出b的值,再代入代数式进行计算即可.
解答 解:∵$\sqrt{{a}^{2}-4}$与$\sqrt{4-{a}^{2}}$有意义,
∴$\left\{\begin{array}{l}{a}^{2}-4≥0\\ 4-{a}^{2}≥0\end{array}\right.$,解得a=±2,
∵a-2≠0,
∴a=-2,
∴a=-2,b为任意实数;
(1)ba=b-2=$\frac{1}{b}$(b≠0);
(2)(a+b)2015=(b-2)2015.
点评 本题考查的是二次根式有意义的条件,熟知二次根式具有非负性是解答此题的关键.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
11.a14可以写成( )
| A. | a7+a7 | B. | a7•a7 | C. | a5•a8 | D. | a8•a2 |
18.下列分解因式正确的是( )
| A. | m2+n2=(m+n)2 | B. | 16m2-4n2=(4m-n)(4m+2n) | ||
| C. | a3-3a2+a=a(a2-3a) | D. | 4a2-4ab+b2=(2a-b)2 |
8.某家具厂销售1套A种款式和2套B种款式的家具的利润为1400元,销售2套A种款式和3套B种款式家具的利润为2400元
(1)求每套A种款式和每套B种款式家具的销售利润;
(2)该家具厂计划用甲种板材200m2,乙种板材250m2生产A、B两种款式的家具,每套所需板材情况如表:
设甲种板材全部用完时恰好生产A款家具x套,两种款式家具全部售完时的销售利润为y元.
①求y与x之间的函数关系式;
②用这些板材生产的A、B两款家具,最大销售利润是多少?
(1)求每套A种款式和每套B种款式家具的销售利润;
(2)该家具厂计划用甲种板材200m2,乙种板材250m2生产A、B两种款式的家具,每套所需板材情况如表:
| 甲种板材(m2) | 乙种板材(m2) | |
| A款 | 3 | 6 |
| B款 | 5 | 4 |
①求y与x之间的函数关系式;
②用这些板材生产的A、B两款家具,最大销售利润是多少?
15.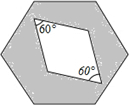 如图,边长为a的正六边形,里面有一菱形,边长也为a,空白部分面积为S1,阴影部分面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$=( )
如图,边长为a的正六边形,里面有一菱形,边长也为a,空白部分面积为S1,阴影部分面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$=( )
 如图,边长为a的正六边形,里面有一菱形,边长也为a,空白部分面积为S1,阴影部分面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$=( )
如图,边长为a的正六边形,里面有一菱形,边长也为a,空白部分面积为S1,阴影部分面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$=( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{3}}{6}$ | D. | $\frac{\sqrt{3}}{9}$ |
 如图,有一个长、宽、高分别为50cm、40cm、30cm的木箱,你能把一根最长为50$\sqrt{2}$cm的木棒放进去.
如图,有一个长、宽、高分别为50cm、40cm、30cm的木箱,你能把一根最长为50$\sqrt{2}$cm的木棒放进去.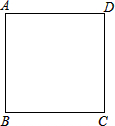 如图,四边形ABCD是一个正方形,
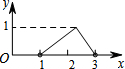
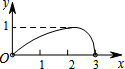
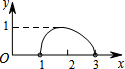
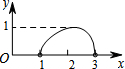
如图,四边形ABCD是一个正方形,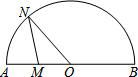 如图,点N是以O为圆心,AB为直径的半圆上的动点,(不与点A,B重合),AB=4,M是OA的中点,设线段MN的长为x,△MNO的面积为y,那么下列图象中,能表示y与x的函数关系的图象大致是( )
如图,点N是以O为圆心,AB为直径的半圆上的动点,(不与点A,B重合),AB=4,M是OA的中点,设线段MN的长为x,△MNO的面积为y,那么下列图象中,能表示y与x的函数关系的图象大致是( )