题目内容
14. 如图,有一个长、宽、高分别为50cm、40cm、30cm的木箱,你能把一根最长为50$\sqrt{2}$cm的木棒放进去.
如图,有一个长、宽、高分别为50cm、40cm、30cm的木箱,你能把一根最长为50$\sqrt{2}$cm的木棒放进去.
分析 根据题意画出图形,首先利用勾股定理计算出BC的长,再利用勾股定理计算出AB的长即可.
解答 解:如图:
∵侧面对角线BC2=302+402=502,
∴CB=50cm,
∵AC=50cm,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}=\sqrt{5{0}^{2}+5{0}^{2}}=50\sqrt{2}$(cm),
∴空木箱能放的最大长度为50$\sqrt{2}$cm.
故答案为50$\sqrt{2}$.
点评 此题主要考查了勾股定理的应用,关键是掌握勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.

练习册系列答案
相关题目
5.已知△ABC中,∠A=90°,角平分线BE,CF交于点O,则∠BOC等于( )
| A. | 135° | B. | 90° | C. | 45° | D. | 145° |
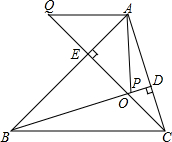 如图,在△ABC中,BD、CE分别是△ABC的高,在BD上取一点P,使BP=AC,在CE的延长线上取一点Q,使CQ=AB,连接AQ与AP.
如图,在△ABC中,BD、CE分别是△ABC的高,在BD上取一点P,使BP=AC,在CE的延长线上取一点Q,使CQ=AB,连接AQ与AP.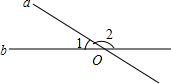 如图,已知直线a、b相交于点O,若∠2=2∠1,则∠1的度数是60°.
如图,已知直线a、b相交于点O,若∠2=2∠1,则∠1的度数是60°.