题目内容
12.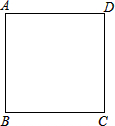 如图,四边形ABCD是一个正方形,
如图,四边形ABCD是一个正方形,(1)请你在平面内找到一点O,并连接OA、OB、OC、OD,使得到的△OAB、△BOC、△COD、△OAD都是等腰三角形.
(2)这样的点你能找到多少个?
(3)写出你找到的等腰三角形的顶角的度数.
分析 (1)连接BC,AD交于一点,则根据正方形的对角线相等的性质,OA=OB=OC=OD且AC⊥BD,可以得△OAB≌△0BC≌△OCD≌△OAD;
(2)对角线交点O只有一个;
(3)该等腰三角形的顶角为∠AOB=90°
解答 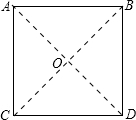 解:(1)连接BC,AD,BC、AD交于O点,
解:(1)连接BC,AD,BC、AD交于O点,
则OA=OB=OC=OD,
且∠AOB=∠BOC=∠COD=∠DOA,
∴△OAB≌△0BC≌△OCD≌△OAD,
故对角线交点O即为所求O点;
(2)这样的点有5个;
(3)△OAB中,∠AOB=90°,OA=OB,
∴要求的等腰三角形顶角为90°,
还有150°,60°,30°.
点评 本题考查了正方形对角线相等、垂直且互相平分的性质,考查了等腰直角三角形顶角为90°的性质,本题中准确的找出O点是解题的关键.

练习册系列答案
相关题目
 甲、乙两车从A城出发前往B城,在整个行程中,汽车离开A城的距离y与时刻t的对应关系如图所示,请根据图象提供的信息完成下列问题:
甲、乙两车从A城出发前往B城,在整个行程中,汽车离开A城的距离y与时刻t的对应关系如图所示,请根据图象提供的信息完成下列问题: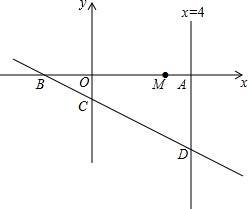 平面直角坐标系中,直线y=-$\frac{1}{2}$x-1与x轴和y轴分别交于B、C两点,与直线x=4交于点D,直线x=4与x轴交于点A,点M(3,0),点E为直线x=4上一动点,点F为直线y=-$\frac{1}{2}$x-1上一动点,ME+EF最小值为$\frac{7\sqrt{5}}{5}$,此时点F的坐标为($\frac{18}{5}$,-$\frac{14}{5}$).
平面直角坐标系中,直线y=-$\frac{1}{2}$x-1与x轴和y轴分别交于B、C两点,与直线x=4交于点D,直线x=4与x轴交于点A,点M(3,0),点E为直线x=4上一动点,点F为直线y=-$\frac{1}{2}$x-1上一动点,ME+EF最小值为$\frac{7\sqrt{5}}{5}$,此时点F的坐标为($\frac{18}{5}$,-$\frac{14}{5}$).