题目内容
13.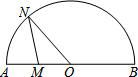 如图,点N是以O为圆心,AB为直径的半圆上的动点,(不与点A,B重合),AB=4,M是OA的中点,设线段MN的长为x,△MNO的面积为y,那么下列图象中,能表示y与x的函数关系的图象大致是( )
如图,点N是以O为圆心,AB为直径的半圆上的动点,(不与点A,B重合),AB=4,M是OA的中点,设线段MN的长为x,△MNO的面积为y,那么下列图象中,能表示y与x的函数关系的图象大致是( )| A. | 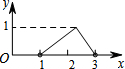 | B. | 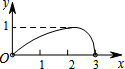 | C. | 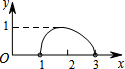 | D. | 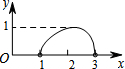 |
分析 先求出自变量x的取值范围是1<x<3,得出B选项错误;再连结AN,BN,过点N作NP⊥AB于P,求出y与x的函数关系式为y=$\frac{\sqrt{-({x}^{2}-5)^{2}+16}}{4}$,进而判断D选项正确.
解答 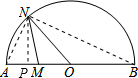 解:∵AB=4,
解:∵AB=4,
∴OA=OB=2,
∵M是OA的中点,
∴OM=AM=1,
∵点N是以O为圆心,AB为直径的半圆上的动点,(不与点A,B重合),线段MN的长为x,
∴1<x<3,故B选项错误;
连结AN,BN,过点N作NP⊥AB于P,∠ANB=90°,
设PM=a,则AP=1-a,BP=a+3.
易证△ANP∽△NBP,
∴$\frac{NP}{BP}$=$\frac{AP}{NP}$,
∴NP2=AP•BP=(1-a)(a+3)=-a2-2a+3,
∵NP2=MN2-PM2=x2-a2,
∴x2-a2=-a2-2a+3,
∴a=$\frac{3-{x}^{2}}{2}$,
∴NP2=x2-a2=x2-($\frac{3-{x}^{2}}{2}$)2=$\frac{{-x}^{4}+10{x}^{2}-9}{4}$=$\frac{-({x}^{2}-5)^{2}+16}{4}$,
∵y=$\frac{1}{2}$OM•NP=$\frac{1}{2}$×1×$\frac{\sqrt{-({x}^{2}-5)^{2}+16}}{2}$=$\frac{\sqrt{-({x}^{2}-5)^{2}+16}}{4}$,
∴当x=$\sqrt{5}$时,NP有最大值2,此时y最大=1.
A选项中,y与x是一次函数关系,不符合题意;
C选项中,y取最大值时,x<2,不符合题意;
只有D选项符合题意.
故选D.
点评 本题考查了动点问题的函数图象,求出y与x的函数关系式是解题的关键,有一定难度.

 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案| A. | 13 | B. | 5 | C. | $\sqrt{129}$ | D. | $\sqrt{119}$ |
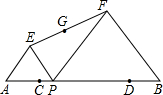 已知线段AB=10,C.D是AB上两点,且AC=DB=2,P是线段CD上一动点,在AB同侧分别作等边三角形APE和等边三角形PBF,G为线段EF的中点,点P由点C移动到点D时,G点移动的路径长度为3.
已知线段AB=10,C.D是AB上两点,且AC=DB=2,P是线段CD上一动点,在AB同侧分别作等边三角形APE和等边三角形PBF,G为线段EF的中点,点P由点C移动到点D时,G点移动的路径长度为3.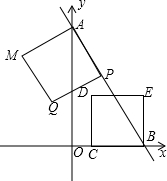 如图,直线y=-$\frac{4}{3}$x+4与坐标轴交于A、B两点,动点P、C以1个单位每秒相同的速度同时分别沿射线AB、BO方向运动,以AP、BC为边分别作如图的两个正方形APQM、BCDE,设动点P的运动时间为t,当正方形APQM的顶点Q落在正方形BCDE的边所在的直线上时,t的值为$\frac{5}{3}$、$\frac{15}{4}$或$\frac{20}{7}$.
如图,直线y=-$\frac{4}{3}$x+4与坐标轴交于A、B两点,动点P、C以1个单位每秒相同的速度同时分别沿射线AB、BO方向运动,以AP、BC为边分别作如图的两个正方形APQM、BCDE,设动点P的运动时间为t,当正方形APQM的顶点Q落在正方形BCDE的边所在的直线上时,t的值为$\frac{5}{3}$、$\frac{15}{4}$或$\frac{20}{7}$.