题目内容
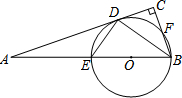 已知:如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,交AC于点D,经过B、D两点的⊙O交AB 于点E,交BC于点F,EB为⊙O的直径.
已知:如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,交AC于点D,经过B、D两点的⊙O交AB 于点E,交BC于点F,EB为⊙O的直径.(1)求证:AC是⊙O的切线;
(2)当BC=2,cos∠ABC=
| 1 |
| 3 |
考点:切线的判定,相似三角形的判定与性质
专题:
分析:(1)根据切线的判定定理,垂直经过半径外端的直线是圆的切线,连接OD,只要得出OD⊥AC即可得出;
(2)通过解直角三角形求得AB,然后证明△AOD∽△ABC,利用相似的性质得对应边的比值相等,即可求得⊙O的半径.
(2)通过解直角三角形求得AB,然后证明△AOD∽△ABC,利用相似的性质得对应边的比值相等,即可求得⊙O的半径.
解答: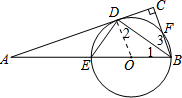 (1)证明:如图,连结OD.
(1)证明:如图,连结OD.
∴OD=OB.
∴∠1=∠2.
∵BD平分∠ABC,
∴∠1=∠3.
∴∠2=∠3.
∴OD∥BC.
∴∠ADO=∠C=90°.
∴OD⊥AC.
∵OD是⊙O的半径,
∴AC是⊙O的切线.
(2)解:在Rt△ACB中,∠C=90,BC=2,cos∠ABC=
,
∴AB=
=6.
设⊙O的半径为r,则AO=6-r.
∵OD∥BC,
∴△AOD∽△ABC.
∴
=
.
∴
=
.
解得 r=
.
∴⊙O的半径为
.
 (1)证明:如图,连结OD.
(1)证明:如图,连结OD.∴OD=OB.
∴∠1=∠2.
∵BD平分∠ABC,
∴∠1=∠3.
∴∠2=∠3.
∴OD∥BC.
∴∠ADO=∠C=90°.
∴OD⊥AC.
∵OD是⊙O的半径,
∴AC是⊙O的切线.
(2)解:在Rt△ACB中,∠C=90,BC=2,cos∠ABC=
| 1 |
| 3 |
∴AB=
| BC |
| cos∠ABC |
设⊙O的半径为r,则AO=6-r.
∵OD∥BC,
∴△AOD∽△ABC.
∴
| OD |
| BC |
| AO |
| AB |
∴
| r |
| 2 |
| 6-r |
| 6 |
解得 r=
| 3 |
| 2 |
∴⊙O的半径为
| 3 |
| 2 |
点评:此题主要考查了切线的判定定理与相似三角形的判定和性质定理,此定理是初中阶段非常重要的定理,同学们应正确把握此定理.

练习册系列答案
相关题目
P1(x1,y1),P2(x2,y2)是正比例函数y=-
x图象上的两点,当x1<x2时,下列判断正确的是( )
| 1 |
| 2 |
| A、y1>y2 |
| B、y1<y2 |
| C、y1=y2 |
| D、无法比较 |
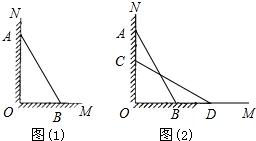 如图(1),一架长为20米云梯AB斜靠在竖直的墙ON上,这时云梯下端B到墙底端O的距离BO=12米,在下列结论中,正确的是( )
如图(1),一架长为20米云梯AB斜靠在竖直的墙ON上,这时云梯下端B到墙底端O的距离BO=12米,在下列结论中,正确的是( )A、当消防员爬到距离地面
| ||
| B、如图(2),当梯子顶端A沿墙下滑3米时,底端B向外移动3米 | ||
| C、如图(2),在梯子下滑过程中,梯子AB与墙ON,地面OM构成的三角形面积存在最大值,最大值为100米2 | ||
D、若在射线ON上存在一点G,使得△ABG为等腰三角形,则AG=
|
“二次函数y=ax2+bx+c的图象与x轴有两个公共点,那么一元二次方程ax2+bx+c=0有两个不相等的实数根.”请根据对这句话的理解,解决下面问题:若m,n(m<n)是关于x的方程2-(x-a)(x-b)=0的两根,且a<b,则a,b,m,n的大小关系是( )
| A、a<m<n<b |
| B、a<m<b<n |
| C、m<a<b<n |
| D、m<a<n<b |
 如图,扇形折扇完全打开后,如果张开的角度(∠BAC)为120°,骨柄AB的长为30cm,扇面的宽度BD的长为20cm,那么这把折扇的扇面面积为( )
如图,扇形折扇完全打开后,如果张开的角度(∠BAC)为120°,骨柄AB的长为30cm,扇面的宽度BD的长为20cm,那么这把折扇的扇面面积为( )A、
| ||
B、
| ||
C、
| ||
| D、300πcm2 |
 如图,在△ABC中,CD⊥AB于D,tanA=2cos∠BCD.
如图,在△ABC中,CD⊥AB于D,tanA=2cos∠BCD.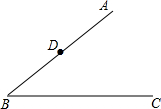 如图,∠ABC的边AB上有一点D.请按下列要求画图并回答问题:
如图,∠ABC的边AB上有一点D.请按下列要求画图并回答问题: