题目内容
“二次函数y=ax2+bx+c的图象与x轴有两个公共点,那么一元二次方程ax2+bx+c=0有两个不相等的实数根.”请根据对这句话的理解,解决下面问题:若m,n(m<n)是关于x的方程2-(x-a)(x-b)=0的两根,且a<b,则a,b,m,n的大小关系是( )
| A、a<m<n<b |
| B、a<m<b<n |
| C、m<a<b<n |
| D、m<a<n<b |
考点:抛物线与x轴的交点
专题:
分析:依题意画出函数y=(x-a)(x-b)图象草图,根据二次函数的增减性求解.
解答: 解:依题意,画出函数y=(x-a)(x-b)的图象,如图所示.
解:依题意,画出函数y=(x-a)(x-b)的图象,如图所示.
函数图象为抛物线,开口向上,与x轴两个交点的横坐标分别为a,b(a<b).
方程2-(x-a)(x-b)=0
转化为(x-a)(x-b)=2,
方程的两根是抛物线y=(x-a)(x-b)与直线y=2的两个交点.
由m<n,可知对称轴左侧交点横坐标为m,右侧为n.
由抛物线开口向上,则在对称轴左侧,y随x增大而减少,则有m<a;在对称轴右侧,y随x增大而增大,则有b<n.
综上所述,可知m<a<b<n.
故选:C.
 解:依题意,画出函数y=(x-a)(x-b)的图象,如图所示.
解:依题意,画出函数y=(x-a)(x-b)的图象,如图所示.函数图象为抛物线,开口向上,与x轴两个交点的横坐标分别为a,b(a<b).
方程2-(x-a)(x-b)=0
转化为(x-a)(x-b)=2,
方程的两根是抛物线y=(x-a)(x-b)与直线y=2的两个交点.
由m<n,可知对称轴左侧交点横坐标为m,右侧为n.
由抛物线开口向上,则在对称轴左侧,y随x增大而减少,则有m<a;在对称轴右侧,y随x增大而增大,则有b<n.
综上所述,可知m<a<b<n.
故选:C.
点评:本题考查了二次函数与一元二次方程的关系,考查了数形结合的数学思想.解题时,画出函数草图,由函数图象直观形象地得出结论,避免了繁琐复杂的计算.

练习册系列答案
相关题目
已知非零向量
、
和
,下列条件中,不能判定
∥
的是( )
| a |
| b |
| c |
| a |
| b |
A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、|
|
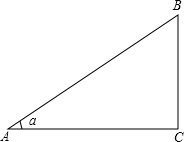 如图:为了测楼房BC的高,在距离楼房10米的A处,测得楼顶B的仰角为,那么楼房BC的高为( )
如图:为了测楼房BC的高,在距离楼房10米的A处,测得楼顶B的仰角为,那么楼房BC的高为( )| A、10tana(米) | ||||||
B、
| ||||||
| C、10sina(米) | ||||||
D、
|
 △ABC中,∠C=Rt∠,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB、BC分别交于点E、D,则AE的长为( )
△ABC中,∠C=Rt∠,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB、BC分别交于点E、D,则AE的长为( )A、
| ||
B、
| ||
C、
| ||
D、
|
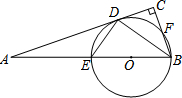 已知:如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,交AC于点D,经过B、D两点的⊙O交AB 于点E,交BC于点F,EB为⊙O的直径.
已知:如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,交AC于点D,经过B、D两点的⊙O交AB 于点E,交BC于点F,EB为⊙O的直径.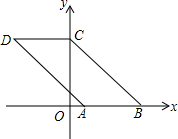 如图,已知点A(1,0),B(4,0),将线段AB平移得到线段CD,点B的对应点C恰好落在y轴上,且四边形ABCD的面积为9,则四边形ABCD的周长为( )
如图,已知点A(1,0),B(4,0),将线段AB平移得到线段CD,点B的对应点C恰好落在y轴上,且四边形ABCD的面积为9,则四边形ABCD的周长为( )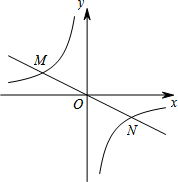 如图,正比例函数y=-
如图,正比例函数y=-