题目内容
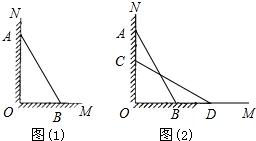 如图(1),一架长为20米云梯AB斜靠在竖直的墙ON上,这时云梯下端B到墙底端O的距离BO=12米,在下列结论中,正确的是( )
如图(1),一架长为20米云梯AB斜靠在竖直的墙ON上,这时云梯下端B到墙底端O的距离BO=12米,在下列结论中,正确的是( )A、当消防员爬到距离地面
| ||
| B、如图(2),当梯子顶端A沿墙下滑3米时,底端B向外移动3米 | ||
| C、如图(2),在梯子下滑过程中,梯子AB与墙ON,地面OM构成的三角形面积存在最大值,最大值为100米2 | ||
D、若在射线ON上存在一点G,使得△ABG为等腰三角形,则AG=
|
考点:勾股定理的应用
专题:
分析:根据勾股定理及相似三角形的性质对各选项进行逐一分析即可.
解答: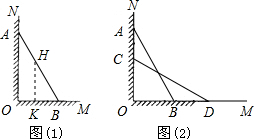 解:∵AB=20米,BO=12米,
解:∵AB=20米,BO=12米,
∴OA=
=16(米).
A、当消防员爬到距离地面
米时,如图1所示,过点H作HK⊥OM,
∵AO⊥OM,
∴△BKH∽△BOA,
∴
=
,即
=
,解得BK=
,
∴OK=12-
=
≠
,故本选项错误;
B、如图(2),当梯子顶端A沿墙下滑3米时,
∵OC=OA-3=16-3=13,
∴OD=
=
=
(米),
∵OD-OB=
-12≠3,故本选项错误;
C、∵当AB移动到OA=OB时,△ABC的面积最大,此时斜边上的高=
AB=10米,
∴S最大=
×20×10=100米2,故本选项正确;
D、∵AB=20,△ABG为等腰三角形,
∴AG=AB=20,故本选项错误.
故选C.
 解:∵AB=20米,BO=12米,
解:∵AB=20米,BO=12米,∴OA=
| 202-122 |
A、当消防员爬到距离地面
| 45 |
| 7 |
∵AO⊥OM,
∴△BKH∽△BOA,
∴
| HK |
| OA |
| BK |
| OB |
| ||
| 16 |
| BK |
| 12 |
| 135 |
| 28 |
∴OK=12-
| 135 |
| 28 |
| 201 |
| 28 |
| 45 |
| 7 |
B、如图(2),当梯子顶端A沿墙下滑3米时,
∵OC=OA-3=16-3=13,
∴OD=
| CD2-OC2 |
| 202-132 |
| 231 |
∵OD-OB=
| 231 |
C、∵当AB移动到OA=OB时,△ABC的面积最大,此时斜边上的高=
| 1 |
| 2 |
∴S最大=
| 1 |
| 2 |
D、∵AB=20,△ABG为等腰三角形,
∴AG=AB=20,故本选项错误.
故选C.
点评:本题考查的是勾股定理的应用,在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.

练习册系列答案
相关题目
已知非零向量
、
和
,下列条件中,不能判定
∥
的是( )
| a |
| b |
| c |
| a |
| b |
A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、|
|
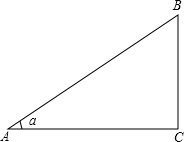 如图:为了测楼房BC的高,在距离楼房10米的A处,测得楼顶B的仰角为,那么楼房BC的高为( )
如图:为了测楼房BC的高,在距离楼房10米的A处,测得楼顶B的仰角为,那么楼房BC的高为( )| A、10tana(米) | ||||||
B、
| ||||||
| C、10sina(米) | ||||||
D、
|
如果4x=5y(y≠0),那么下列比例式成立的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图是正方体的展开图,若此正方体相对面上的数互为相反数,求a-(b-c)的值.
如图是正方体的展开图,若此正方体相对面上的数互为相反数,求a-(b-c)的值.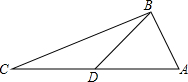 如图,在△ABC中,AB=5,BC=12,AC=13,点D是AC的中点,则BD=
如图,在△ABC中,AB=5,BC=12,AC=13,点D是AC的中点,则BD=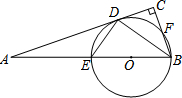 已知:如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,交AC于点D,经过B、D两点的⊙O交AB 于点E,交BC于点F,EB为⊙O的直径.
已知:如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,交AC于点D,经过B、D两点的⊙O交AB 于点E,交BC于点F,EB为⊙O的直径.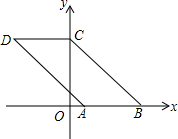 如图,已知点A(1,0),B(4,0),将线段AB平移得到线段CD,点B的对应点C恰好落在y轴上,且四边形ABCD的面积为9,则四边形ABCD的周长为( )
如图,已知点A(1,0),B(4,0),将线段AB平移得到线段CD,点B的对应点C恰好落在y轴上,且四边形ABCD的面积为9,则四边形ABCD的周长为( )