题目内容
已知数轴上点A、B表示的数分别为-1、3、p为数轴上一动点,其表示的数为x.
(1)若P到A、B的距离相等,则x= ;
(2)是否存在点P,使PA+PB=6?若存在,写出x的值;若不存在,请说明理由;
(3)若点M、N分别从A、B同时出发,沿数轴正方向分别以2个单位/秒、1个单位/秒的速度运动,则经过多长时间,M、N两点相距1个单位长度?

(1)若P到A、B的距离相等,则x=
(2)是否存在点P,使PA+PB=6?若存在,写出x的值;若不存在,请说明理由;
(3)若点M、N分别从A、B同时出发,沿数轴正方向分别以2个单位/秒、1个单位/秒的速度运动,则经过多长时间,M、N两点相距1个单位长度?

考点:一元一次方程的应用,数轴
专题:
分析:(1)要使P到A、B的距离相等,则x=1;
(2)分别表示出PA、PB,令PA+PB=6,代入求出x的值;
(3)设t秒后M、N两点相距1个单位长度,表示出MN的长度,令MN=1,求出t的值.
(2)分别表示出PA、PB,令PA+PB=6,代入求出x的值;
(3)设t秒后M、N两点相距1个单位长度,表示出MN的长度,令MN=1,求出t的值.
解答:解:(1)由图可得,x=1;
(2)PA=|-1-x|,PB=|3-x|,
则PA+PB=|-1-x|+|3-x|,
当x≤-1时,-1-x+3-x=6,
解得:x=-2;
当-1<x<3时,x+1+3-x=6,
无解;
当x≥3时,x+1+x-3=6,
解得:x=4;
(3)设t秒后M、N两点相距1个单位长度,
MN=|(-1+2t)-(3+t)|=1,
|t-4|=1,
当t>4时,t-4=1,
解得:t=5,
当t≤4时,4-t=1,
解得:t=3.
答:经过3s或5s,M、N两点相距1个单位长度.
故答案为:1.
(2)PA=|-1-x|,PB=|3-x|,
则PA+PB=|-1-x|+|3-x|,
当x≤-1时,-1-x+3-x=6,
解得:x=-2;
当-1<x<3时,x+1+3-x=6,
无解;
当x≥3时,x+1+x-3=6,
解得:x=4;
(3)设t秒后M、N两点相距1个单位长度,
MN=|(-1+2t)-(3+t)|=1,
|t-4|=1,
当t>4时,t-4=1,
解得:t=5,
当t≤4时,4-t=1,
解得:t=3.
答:经过3s或5s,M、N两点相距1个单位长度.
故答案为:1.
点评:本题考查了一元一次方程的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程求解.

练习册系列答案
相关题目
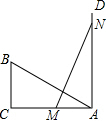 如图,在△ABC中,∠C=90°,AB=2,BC=1,射线AD⊥AC,M为AC上的动点,N为射线AD上的动点,点M,N分别在AC,AD上运动,且始终保持MN=AB,当△ABC与△AMN全等时,此时AM的长为( )
如图,在△ABC中,∠C=90°,AB=2,BC=1,射线AD⊥AC,M为AC上的动点,N为射线AD上的动点,点M,N分别在AC,AD上运动,且始终保持MN=AB,当△ABC与△AMN全等时,此时AM的长为( )| A、1 | ||
B、
| ||
| C、2 | ||
D、1或
|
如果4x=5y(y≠0),那么下列比例式成立的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
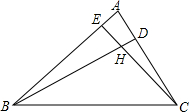 如图,BD,CE分别是△ABC的两条高、它们相交于点H,那么下列式子中正确的有( )个.
如图,BD,CE分别是△ABC的两条高、它们相交于点H,那么下列式子中正确的有( )个.(1)∠DHC=∠A;(2)∠EBH+∠A=90°;(3)∠ACE=∠ABD;(4)∠ECB=∠ABC.
| A、1 | B、2 | C、3 | D、4 |
 △ABC中,∠C=Rt∠,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB、BC分别交于点E、D,则AE的长为( )
△ABC中,∠C=Rt∠,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB、BC分别交于点E、D,则AE的长为( )A、
| ||
B、
| ||
C、
| ||
D、
|
若数据8,7,7,6,5,5,x的平均数是6,则这组数据的中位数是( )
| A、5 | B、5.5 | C、6 | D、7 |
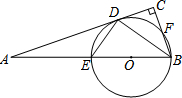 已知:如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,交AC于点D,经过B、D两点的⊙O交AB 于点E,交BC于点F,EB为⊙O的直径.
已知:如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,交AC于点D,经过B、D两点的⊙O交AB 于点E,交BC于点F,EB为⊙O的直径. 如图,点A,B,C,D为⊙O上的四个点,AC交BD于点E,∠DAC=∠BDC,CE=4,CD=6,则AE的长为( )
如图,点A,B,C,D为⊙O上的四个点,AC交BD于点E,∠DAC=∠BDC,CE=4,CD=6,则AE的长为( )