题目内容
如图，在△ABC中，CD⊥AB于D，tanA=2cos∠BCD．（1）求证：BC=2AD；
（2）若cosB=
| 3 |
| 4 |
考点：解直角三角形
专题：
分析：（1）由tanA=2cos∠BCD即可求得结论；
（2）由∠B的余弦值和（1）的结论即可求得BD，利用勾股定理求得CD．
（2）由∠B的余弦值和（1）的结论即可求得BD，利用勾股定理求得CD．
解答：解：（1）∵tanA=
，cos∠BCD=
，tanA=2cos∠BCD，
∴
=2×
，
∴BC=2AD；
（2）∵cosB=
=
，BC=2AD，
∴
=
，
∵AB=10，
∴AD=
×10=4，BD=10-4=6，
∴BC=8，
∴CD=
=2
．
| CD |
| AD |
| CD |
| BC |
∴
| CD |
| AD |
| CD |
| BC |
∴BC=2AD；
（2）∵cosB=
| BD |
| BC |
| 3 |
| 4 |
∴
| BD |
| AD |
| 3 |
| 2 |
∵AB=10，
∴AD=
| 2 |
| 5 |
∴BC=8，
∴CD=
| BC2-BD2 |
| 7 |
点评：本题考查了直角三角形中的有关问题，主要考查了勾股定理，三角函数的有关计算．
练习册系列答案
相关题目
近似数0.38万精确到（ ）
| A、十分位 | B、百位 | C、千位 | D、万位 |
850000000000用科学记数法表示为（ ）
| A、8.5×103亿 |
| B、0.85×104亿 |
| C、8.5×104亿 |
| D、85×102亿 |
已知非零向量
、
和
，下列条件中，不能判定
∥
的是（ ）
| a |
| b |
| c |
| a |
| b |
A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、|
|
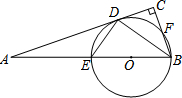已知：如图，在Rt△ABC中，∠C=90°，BD平分∠ABC，交AC于点D，经过B、D两点的⊙O交AB 于点E，交BC于点F，EB为⊙O的直径．
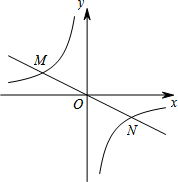如图，正比例函数y=-
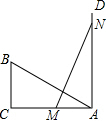如图，在△ABC中，∠C=90°，AB=2，BC=1，射线AD⊥AC，M为AC上的动点，N为射线AD上的动点，点M，N分别在AC，AD上运动，且始终保持MN=AB，当△ABC与△AMN全等时，此时AM的长为（ ）