题目内容
14.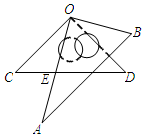 如图,将一副三角板叠放在一起,使直角的顶点重合于点O,AB∥OC,CD与OA交于点E,已知∠A=30°,则∠DEO的度数为( )
如图,将一副三角板叠放在一起,使直角的顶点重合于点O,AB∥OC,CD与OA交于点E,已知∠A=30°,则∠DEO的度数为( )| A. | 45° | B. | 60° | C. | 70° | D. | 75° |
分析 由平行线的性质求出∠AOC=30°,再根据三角形的外角性质即可得出结论.
解答 解:∵AB∥OC,∠A=30°,
∴∠AOC=∠A=30°,
∵∠DEO是△CEO的外角,
∴∠DEO=∠C+∠AOC=45°+30°=75°,
故选:D.
点评 本题主要考查了平行线的性质、三角形的外角性质;熟练掌握平行线的性质和三角形的外角性质是解决问题的关键.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
2.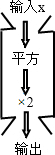 如图是一组数值转换机,若它输出的结果为32,则输入值为( )
如图是一组数值转换机,若它输出的结果为32,则输入值为( )
 如图是一组数值转换机,若它输出的结果为32,则输入值为( )
如图是一组数值转换机,若它输出的结果为32,则输入值为( )| A. | ±8 | B. | 8 | C. | ±4 | D. | 4 |
6. 如图,在△ABC中,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、补角∠ACF,下列结论:①AD∥BC;②∠ACB=2∠ADB;③∠DCF=∠BDC+∠ABD;④∠BDC=∠BAC,其中正确的结论有( )
如图,在△ABC中,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、补角∠ACF,下列结论:①AD∥BC;②∠ACB=2∠ADB;③∠DCF=∠BDC+∠ABD;④∠BDC=∠BAC,其中正确的结论有( )
 如图,在△ABC中,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、补角∠ACF,下列结论:①AD∥BC;②∠ACB=2∠ADB;③∠DCF=∠BDC+∠ABD;④∠BDC=∠BAC,其中正确的结论有( )
如图,在△ABC中,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、补角∠ACF,下列结论:①AD∥BC;②∠ACB=2∠ADB;③∠DCF=∠BDC+∠ABD;④∠BDC=∠BAC,其中正确的结论有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
4.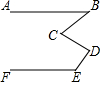 如图,AB∥EF,则下列关系中正确的是( )
如图,AB∥EF,则下列关系中正确的是( )
 如图,AB∥EF,则下列关系中正确的是( )
如图,AB∥EF,则下列关系中正确的是( )| A. | ∠C=∠B+∠D | B. | ∠D+∠E=180°+∠B | ||
| C. | ∠B+∠D+∠E=180°+∠C | D. | ∠E+∠B=∠C+∠D |
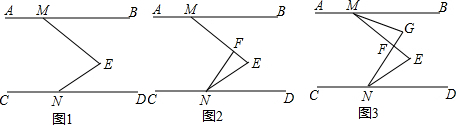
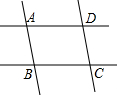 如图,①如果AD∥BC,那么根据两直线平行,同旁内角互补,得∠BAD+∠ABC=180°;②如果AB∥CD,那么根据两直线平行,同旁内角互补,得∠BCD+∠ABC=180°.
如图,①如果AD∥BC,那么根据两直线平行,同旁内角互补,得∠BAD+∠ABC=180°;②如果AB∥CD,那么根据两直线平行,同旁内角互补,得∠BCD+∠ABC=180°.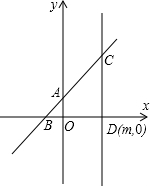 如图,经过点D(m,0)作y轴的平行线n,交一次函数y=x+1的图象于C,函数y=x+1的图象与x、y轴分别相交于B、A.(其中m>0)
如图,经过点D(m,0)作y轴的平行线n,交一次函数y=x+1的图象于C,函数y=x+1的图象与x、y轴分别相交于B、A.(其中m>0)