题目内容
4．
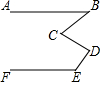如图，AB∥EF，则下列关系中正确的是（ ）| A． | ∠C=∠B+∠D | B． | ∠D+∠E=180°+∠B | ||
| C． | ∠B+∠D+∠E=180°+∠C | D． | ∠E+∠B=∠C+∠D |
分析 延长BC交EF于一点，根据平行线的性质可得∠1=∠B，再根据四边形内角和可得∠1+∠2+∠D+∠E=360°，然后利用等量代换可得答案．
解答 
解：延长BC交EF于一点，
∵AB∥EF，
∴∠1=∠B，
∵∠1+∠2+∠D+∠E=360°，
∴∠B+（180-∠C）+∠D+∠E=360°，
∴∠B+∠D+∠E=180°+∠C，
故选：C．
点评 此题主要考查了平行线的性质，关键是掌握两直线平行，内错角相等．
练习册系列答案
阅读快车系列答案
相关题目
14．
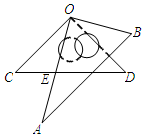如图，将一副三角板叠放在一起，使直角的顶点重合于点O，AB∥OC，CD与OA交于点E，已知∠A=30°，则∠DEO的度数为（ ）
如图，将一副三角板叠放在一起，使直角的顶点重合于点O，AB∥OC，CD与OA交于点E，已知∠A=30°，则∠DEO的度数为（ ）| A． | 45° | B． | 60° | C． | 70° | D． | 75° |
15．
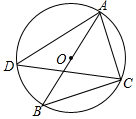如图，⊙O的直径AB=2，点C、D在⊙O上，∠ADC=30°，则BC的长为（ ）
如图，⊙O的直径AB=2，点C、D在⊙O上，∠ADC=30°，则BC的长为（ ）| A． | $\sqrt{2}$ | B． | $\sqrt{3}$ | C． | 2 | D． | 1 |
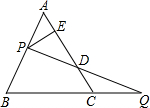如图所示，等边三角形ABC的边长是6，点P在边AB上，点Q在BC的延长线上，且AP=CQ，设PQ与AC相交于点D．
如图，在一块长为30米，宽为16米的长方形草地上，有两条宽都为1米的纵、横相交的小路，这块草地的绿地面积为435平方米．
如图，△ABC的周长为21cm，边AC的垂直平分线为DE交BC于点D，E为垂足，AE=3cm，则△ABD的周长是15cm．