题目内容
2．
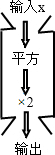如图是一组数值转换机，若它输出的结果为32，则输入值为（ ）| A． | ±8 | B． | 8 | C． | ±4 | D． | 4 |
分析 根据转换机列出方程，再根据平方根的定义解答即可．
解答 解：由题意得，x2×2=32，
所以，x2=16，
∵（±4）2=16，
∴x=±4．
故选C．
点评 此题考查了有理数的混合运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
13．
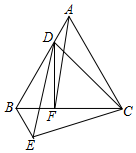如图，点D是等边△ABC的边AB上一点，连接CD并以CD为边作等边△CDE，连接BE，过D作DF⊥BC于F，连AF．若AF∥DE，BC=4，则CF的长度为（ ）
如图，点D是等边△ABC的边AB上一点，连接CD并以CD为边作等边△CDE，连接BE，过D作DF⊥BC于F，连AF．若AF∥DE，BC=4，则CF的长度为（ ）| A． | 2 | B． | $\frac{7}{3}$ | C． | $\frac{8}{3}$ | D． | 3 |
10．x是一个两位数，y是一个一位数，如果把y放在x的左边组成一个三位数，则此三位数可表示为（ ）
| A． | yx | B． | y+x | C． | 10y+x | D． | 100y+x |
17．已知平行四边形ABCD的周长为42，自顶点D作DE⊥AB于E，DF⊥BC于F，若DE=3，DF=4，则BE+BF的长为（ ）
| A． | 21-14$\sqrt{2}$ | B． | 21+14$\sqrt{2}$ | C． | 21+14$\sqrt{2}$或21-14$\sqrt{2}$ | D． | 3+2$\sqrt{2}$或21+14$\sqrt{2}$ |
14．
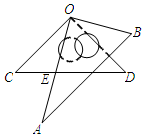如图，将一副三角板叠放在一起，使直角的顶点重合于点O，AB∥OC，CD与OA交于点E，已知∠A=30°，则∠DEO的度数为（ ）
如图，将一副三角板叠放在一起，使直角的顶点重合于点O，AB∥OC，CD与OA交于点E，已知∠A=30°，则∠DEO的度数为（ ）| A． | 45° | B． | 60° | C． | 70° | D． | 75° |
11．如果一条抛物线y=ax2+bx+c（a≠0）与x轴有两个交点，那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”，[a，b，c]称为“抛物线三角形系数”．若抛物线三角形系数为[-1，b，0]的“抛物线三角形”是等边三角形，则b的值为（ ）
| A． | ±2$\sqrt{3}$ | B． | ±$\frac{2\sqrt{3}}{3}$ | C． | 2$\sqrt{3}$ | D． | $\frac{2\sqrt{3}}{3}$ |