题目内容
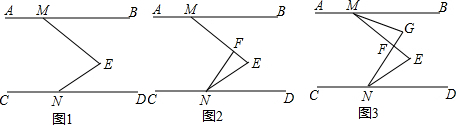
4.如图,M,N分别是直线AB,CD上一点,点E在直线AB,CD之间,∠BME+∠DNE=∠E.(1)如图一,求证:AB∥CD;
(2)F是EM上一点,NE平分∠FND.
①如图2,若∠FNE=∠BME,∠E=60°,求证:NF⊥ME;
②如图3,延长NF交∠BME的角平分线MG于G,探究∠E,∠G与∠MFN之间有何数量关系?并证明你的结论.
分析 (1)过点E做EF∥AB,则∠BME=∠MEF,由∠E=∠MEF+∠NEF、∠BME+∠DNE=∠E可得出∠NEF=∠DNE,利用“内错角相等,两直线平行”可证出EF∥CD,进而可得出AB∥CD;
(2)①设∠FNE=∠BME=x,则∠END=60°-x,由角平分线的性质结合(1)的结论可得出关于x的一元一次方程,解之可得出x的值,再根据三角形外角的性质可求出∠MFN=90°,即NF⊥ME;
②设∠BMG=∠EMG=α、∠DNE=∠GNE=β,由(1)的结论可得出∠MFN=2α+2β、∠G=α+2β、∠E=2α+β,进而即可得出∠MFN=$\frac{2}{3}$(∠G+∠E).
解答 (1)证明:在图1中,过点E做EF∥AB,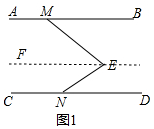
∵EF∥AB,
∴∠BME=∠MEF.
∵∠E=∠MEF+∠NEF,∠BME+∠DNE=∠E,
∴∠NEF=∠DNE,
∴EF∥CD,
∴AB∥CD.
(2)①证明:设∠FNE=∠BME=x,则∠END=60°-x.
∵NE平分∠FND,
∴∠END=∠FNE=x,
即60°-x=x,解得:x=30°.
又∵∠MFN=∠BME+∠FND=x+(x+60°-x)=90°,
∴NF⊥ME.
②解:∠MFN=$\frac{2}{3}$(∠G+∠E),
证明:设∠BMG=∠EMG=α,∠DNE=∠GNE=β,则∠MFN=2α+2β,∠G=α+2β,∠E=2α+β,
∴∠MFN=$\frac{2}{3}$(3α+3β)=$\frac{2}{3}$(∠G+∠E).
点评 本题考查了平行线的判定与性质、角平分线的性质以及三角形外角的性质,解题的关键是:(1)过点E做EF∥AB,证出EF∥CD;(2)①根据角平分线的性质结合(1)的结论,列出关于x的一元一次方程;②利用(1)的结论找出∠MFN=2α+2β、∠G=α+2β、∠E=2α+β.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| x(元) | 180 | 200 | 220 | … |
| y (件) | 850 | 750 | 650 | … |
(2)求销售价定为240元时,每月的销售利润.
| A. | (x+1)2+4 | B. | (x-1)2+2 | C. | (x-1)2+4 | D. | (x+1)2+2 |
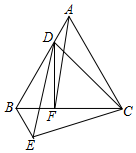 如图,点D是等边△ABC的边AB上一点,连接CD并以CD为边作等边△CDE,连接BE,过D作DF⊥BC于F,连AF.若AF∥DE,BC=4,则CF的长度为( )
如图,点D是等边△ABC的边AB上一点,连接CD并以CD为边作等边△CDE,连接BE,过D作DF⊥BC于F,连AF.若AF∥DE,BC=4,则CF的长度为( )| A. | 2 | B. | $\frac{7}{3}$ | C. | $\frac{8}{3}$ | D. | 3 |
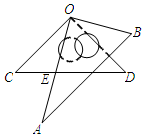 如图,将一副三角板叠放在一起,使直角的顶点重合于点O,AB∥OC,CD与OA交于点E,已知∠A=30°,则∠DEO的度数为( )
如图,将一副三角板叠放在一起,使直角的顶点重合于点O,AB∥OC,CD与OA交于点E,已知∠A=30°,则∠DEO的度数为( )| A. | 45° | B. | 60° | C. | 70° | D. | 75° |