题目内容
3.在农村的“村村通”的道路改键工程中,某路段长4000米,由甲、乙两个工程队拟在30天内(含30天)合作完成,已知两个工程队各有10名工人,设甲、乙两个工程队的工人全部参与生产,且甲、乙两个工程队每天各自的工作量相同,甲工程队1天,乙工程队2天共修路200米,甲工程队2天,乙工程队3天共修路350米.(1)求甲、乙两个工程队每天分别修路多少米?
(2)甲、乙两个工程队施工10天后,由于工作需要,需从甲队抽调m人去学校新技术,总部要求在规定时间内完成,求甲队可以抽调多少人?
(3)已知甲工程队每天的施工费用为0.6万元,乙工程队每天的施工费用为0.35万元,要使该工程的施工费用最低,则甲、乙两个工程队各做多少天?最低费用为多少?
分析 (1)设甲队每天修路x米,乙队每天修路y米,然后根据两队修路的长度分别为200米和350米两个等量关系列出方程组,然后解方程组即可得解;
(2)根据甲队抽调m人后两队所修路的长度不小于4000米,列出一元一次不等式,然后求出m的取值范围,再根据m是正整数解答;
(3)设甲工程队修a天,乙工程队修b天,根据所修路的长度为4000米列出方程整理并用a表示出b,再根据0≤b≤30表示出a的取值范围,再根据总费用等于两队的费用之和列式整理,然后根据一次函数的增减性解答.
解答 解:(1)设甲队每天修路x米,乙队每天修路y米,
依题意得$\left\{\begin{array}{l}{x+2y=200}\\{2x+3y=350}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=100}\\{y=50}\end{array}\right.$.
答:甲工程队每天修路100米,乙工程队每天修路50米;
(2)依题意得,10×100+20×$\frac{10-m}{10}$×100+30×50≥4000,
解得m≤$\frac{5}{2}$,
∵0<m<10,
∴0<m≤$\frac{5}{2}$,
∵m为正整数,
∴m=1或2,
∴甲队可以抽调1人或2人;
(3)设甲工程队修a天,乙工程队修b天,
依题意得,100a+50b=4000,
所以,b=80-2a,
∵0≤b≤30,
∴0≤80-2a≤30,
解得25≤a≤40,
又∵0≤a≤30,
∴25≤a≤30,
设总费用为W元,依题意得,
W=0.6a+0.35b,
=0.6a+0.35(80-2a),
=-0.1a+28,
∵-0.1<0,
∴当a=30时,W最小=-0.1×30+28=25(万元),
此时b=80-2a=80-2×30=20(天).
答:甲工程队需做30天,乙工程队需做20天,最低费用为25万元.
点评 本题考查了一次函数的应用,二元一次方程组的应用,一元一次不等式的应用,读懂题目信息,理清题中熟练关系,准确找出等量关系与不等量关系分别列出方程组和不等式是解题的关键,(3)先根据总工作量表示出甲乙两个工程队的天数的关系是解题的关键.

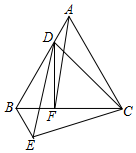 如图,点D是等边△ABC的边AB上一点,连接CD并以CD为边作等边△CDE,连接BE,过D作DF⊥BC于F,连AF.若AF∥DE,BC=4,则CF的长度为( )
如图,点D是等边△ABC的边AB上一点,连接CD并以CD为边作等边△CDE,连接BE,过D作DF⊥BC于F,连AF.若AF∥DE,BC=4,则CF的长度为( )| A. | 2 | B. | $\frac{7}{3}$ | C. | $\frac{8}{3}$ | D. | 3 |
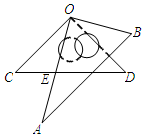 如图,将一副三角板叠放在一起,使直角的顶点重合于点O,AB∥OC,CD与OA交于点E,已知∠A=30°,则∠DEO的度数为( )
如图,将一副三角板叠放在一起,使直角的顶点重合于点O,AB∥OC,CD与OA交于点E,已知∠A=30°,则∠DEO的度数为( )| A. | 45° | B. | 60° | C. | 70° | D. | 75° |
| A. | ±2$\sqrt{3}$ | B. | ±$\frac{2\sqrt{3}}{3}$ | C. | 2$\sqrt{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
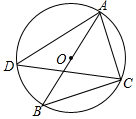 如图,⊙O的直径AB=2,点C、D在⊙O上,∠ADC=30°,则BC的长为( )
如图,⊙O的直径AB=2,点C、D在⊙O上,∠ADC=30°,则BC的长为( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 1 |
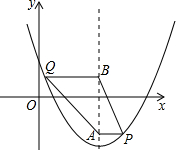 如图,在平面直角坐标系中,抛物线y=x2+bx+c经过点(1,-1),且对称轴为直线x=2,点P、Q均在抛物线上,点P位于对称轴右侧,点Q位于对称轴左侧,PA垂直对称轴于点A,QB垂直对称轴于点B,且QB=PA+1,设点P的横坐标为m.
如图,在平面直角坐标系中,抛物线y=x2+bx+c经过点(1,-1),且对称轴为直线x=2,点P、Q均在抛物线上,点P位于对称轴右侧,点Q位于对称轴左侧,PA垂直对称轴于点A,QB垂直对称轴于点B,且QB=PA+1,设点P的横坐标为m. 如图,△ABC的周长为21cm,边AC的垂直平分线为DE交BC于点D,E为垂足,AE=3cm,则△ABD的周长是15cm.
如图,△ABC的周长为21cm,边AC的垂直平分线为DE交BC于点D,E为垂足,AE=3cm,则△ABD的周长是15cm.