题目内容
9. 如图,已知⊙O是△ABC的外接圆,AB为直径,若PA⊥AB,PO过AC的中点M.
如图,已知⊙O是△ABC的外接圆,AB为直径,若PA⊥AB,PO过AC的中点M.(1)求证:PC是⊙O的切线;
(2)若⊙O的半径长是4,PA=AC,求OM的长.
分析 (1)连接OC,由SSS证明△OPC≌△OPA,得出∠PCO=90°即可;
(2)证明△APC是等边三角形,求出∠BAC=30°,得出BC的长,再证明OM是△ABC的中位线,由三角形中位线定理即可得出结果.
解答 (1)证明:连接OC,如图所示:
∵PA⊥AB,
∴∠PA0=90°.
∵PO过AC的中点M,OA=OC,
∴PO⊥AC,
∴PA=PC,
在△OPC和△OPA中,
$\left\{\begin{array}{l}{PC=PA}&{\;}\\{OC=OA}&{\;}\\{PO=PO}&{\;}\end{array}\right.$,
∴△OPC≌△OPA(SSS),
∴∠PCO=∠PA0=90°,
即OC⊥PO,
∴PC是⊙O的切线.
(2)解:∵⊙O的半径长是4,
∴AB=8,
∵PA=AC,PA=PC,
∴PA=AC=PC,
∴∠PAC=60°,
∴∠BAC=90°-60°=30°,
∴BC=$\frac{1}{2}$AB=4,
∵M是AC的中点,OA=OB,
∴OM是△ABC的中位线,
∴OM=$\frac{1}{2}$BC=2.
点评 本题考查了切线的判定、垂径定理、线段垂直平分线的性质、全等三角形的判定与性质、等边三角形的判定与性质、三角形中位线定理等知识;熟练掌握切线的判定方法,证明三角形全等是解决问题(1)的关键.

练习册系列答案
相关题目
17.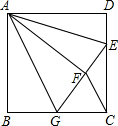 如图,正方形ABCD中,AB=3,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:
如图,正方形ABCD中,AB=3,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:
①点G是BC的中点;
②FG=FC;
③AG∥CF;
④S△FGC=$\frac{9}{10}$.
其中正确结论是( )
 如图,正方形ABCD中,AB=3,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:
如图,正方形ABCD中,AB=3,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①点G是BC的中点;
②FG=FC;
③AG∥CF;
④S△FGC=$\frac{9}{10}$.
其中正确结论是( )
| A. | ①② | B. | ②④ | C. | ①②③ | D. | ①③④ |
10.若(x+2)(x+n)=x2+mx-16,则m+n的值为( )
| A. | -14 | B. | -2 | C. | 2 | D. | 18 |
 如图,在△ABC中,已知AB=AC=5,BC=6,点D、E分别在BC、AC上,且∠ADE=∠B
如图,在△ABC中,已知AB=AC=5,BC=6,点D、E分别在BC、AC上,且∠ADE=∠B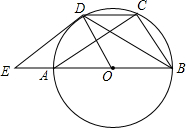 如图,⊙O是△ABC的外接圆,AB是直径,点D是$\widehat{AC}$的中点,E为BA延长线上一点,且∠DEB=∠CDB
如图,⊙O是△ABC的外接圆,AB是直径,点D是$\widehat{AC}$的中点,E为BA延长线上一点,且∠DEB=∠CDB