题目内容
4.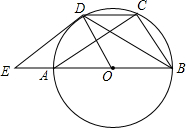 如图,⊙O是△ABC的外接圆,AB是直径,点D是$\widehat{AC}$的中点,E为BA延长线上一点,且∠DEB=∠CDB
如图,⊙O是△ABC的外接圆,AB是直径,点D是$\widehat{AC}$的中点,E为BA延长线上一点,且∠DEB=∠CDB(1)求证:直线ED是⊙O的切线;
(2)若EO=10,BC=9,求⊙O的半径.
分析 (1)根据垂径定理得出OD⊥AC,根据圆周角定理和∠DEB=∠CDB,得出∠DEB=∠CAB,进一步得到ED∥AC,根据平行线的性质求得OD⊥ED,即可证得直线ED是⊙O的切线;
(2)证得△ACB∽△EDO,根据相似三角形的性质即可求得.
解答 (1)证明:∵点D是$\widehat{AC}$的中点,
∴OD⊥AC,
∵∠DEB=∠CDB,∠CDB=∠CAB,
∴∠DEB=∠CAB,
∴ED∥AC,
∴OD⊥ED,
∴直线ED是⊙O的切线;
(2)解:∵AB是直径,
∴∠ACB=90°,
∴∠ACB=∠EDO,
∵∠DEB=∠CAB,
∴△ACB∽△EDO,
∴$\frac{AB}{EO}$=$\frac{BC}{OD}$,
∵AB=2OD,EO=10,BC=9,
∴$\frac{2OD}{10}$=$\frac{9}{OD}$,
解得OD=3$\sqrt{5}$,
∴⊙O的半径为3$\sqrt{5}$.
点评 本题考查了切线的判定,垂径定理进而圆周角定理的应用,三角形相似的判定和性质,熟练掌握性质定理是解题的关键.

练习册系列答案
相关题目
15.新学期开学初,王刚同学对部分同学暑假在家做家务的时间进行了抽样调查(时间取整数小时),所得数据统计如下表:
(1)王刚同学抽取样本的容量是多少?
(2)请你根据表中数据补全图中的频数分布直方图;
(3)若该学校有学生1260人,那么大约有多少学生在暑假做家务的时间在40.5~100.5小时之间?
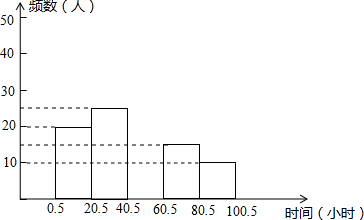
| 时间分组 | 0.5~20.5 | 20.5~40.5 | 40.5~60.5 | 60.5~80.5 | 80.5~100.5 |
| 频 数 | 20 | 25 | 30 | 15 | 10 |
(2)请你根据表中数据补全图中的频数分布直方图;
(3)若该学校有学生1260人,那么大约有多少学生在暑假做家务的时间在40.5~100.5小时之间?

5.若代数式2x-y的值是5,则代数式2y-4x+5的值为( )
| A. | -15 | B. | -5 | C. | 5 | D. | 15 |
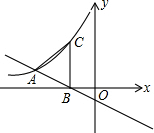 直线y=-$\frac{1}{2}$x-1与反比例函数y=$\frac{k}{x}$(x<0)的图象交于点A,与x轴相交于点B,过点B作x轴垂线交双曲线于点C,若AB=AC,则k的值为-4.
直线y=-$\frac{1}{2}$x-1与反比例函数y=$\frac{k}{x}$(x<0)的图象交于点A,与x轴相交于点B,过点B作x轴垂线交双曲线于点C,若AB=AC,则k的值为-4. 如图,已知⊙O是△ABC的外接圆,AB为直径,若PA⊥AB,PO过AC的中点M.
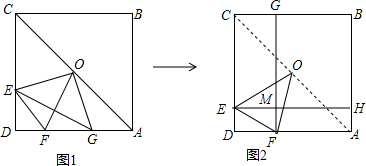
如图,已知⊙O是△ABC的外接圆,AB为直径,若PA⊥AB,PO过AC的中点M.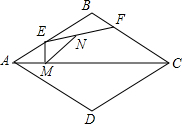 如图,菱形ABCD的边长为8,∠BAD=60°,点E在AB上运动,点F在BC上运动(E,F两点可以和菱形的顶点重合),且EF=4,点N是线段EF的中点,ME⊥AC垂足为M,则MN的最小值是2$\sqrt{3}$.
如图,菱形ABCD的边长为8,∠BAD=60°,点E在AB上运动,点F在BC上运动(E,F两点可以和菱形的顶点重合),且EF=4,点N是线段EF的中点,ME⊥AC垂足为M,则MN的最小值是2$\sqrt{3}$. 如图所示,Rt△ABC中,∠ACB=90°,点A坐标为(0,1),点B坐标为(0,-1),且∠ABC=30°,若反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点C,则k的值为$\frac{\sqrt{3}}{4}$.
如图所示,Rt△ABC中,∠ACB=90°,点A坐标为(0,1),点B坐标为(0,-1),且∠ABC=30°,若反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点C,则k的值为$\frac{\sqrt{3}}{4}$.