题目内容
1.试运用不等式的基本性质分别写出下列不等式的解集.(1)x+3<6;
(2)-2x>8;
(3)3x>9;
(4)2x-1≥6.
分析 (1)由性质1两边都减3可得;
(2)由性质3两边都除以-2得;
(3)根据性质2两边都除以3得;
(4)先根据性质1两边都加3,再根据性质2两边都除以2即可得.
解答 解:(1)移项、合并,得:x<3;
(2)两边都除以-2,得:x<-4;
(3)两边都除以3,得:x>3;
(4)移项、合并,得:2x≥7,
两边都除以2,得:x≥$\frac{7}{2}$.
点评 本题主要考查依据不等式性质解不等式,不等式的基本性质,在不等式的两边同时加上或减去同一个数或整式不等号的方向不变;在不等式的两边同时乘以或除以同一个正数不等号的方向不变;在不等式的两边同时乘以或除以同一个负数不等号的方向改变.特别是在系数化为1这一个过程中要注意不等号的方向的变化.

练习册系列答案
相关题目
11.下列不等式组中,无解的是( )
| A. | $\left\{\begin{array}{l}{x>-3}\\{x>2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x<-3}\\{x<2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x>-3}\\{x<2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x<-3}\\{x>2}\end{array}\right.$ |
2.若代数式y2+y-2的值为0,则代数式y3+4y2+y+2014的值为( )
| A. | 2014 | B. | 2015 | C. | 2020 | D. | 2025 |
 如图,已知⊙O是△ABC的外接圆,AB为直径,若PA⊥AB,PO过AC的中点M.
如图,已知⊙O是△ABC的外接圆,AB为直径,若PA⊥AB,PO过AC的中点M.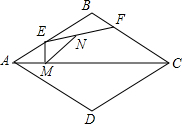 如图,菱形ABCD的边长为8,∠BAD=60°,点E在AB上运动,点F在BC上运动(E,F两点可以和菱形的顶点重合),且EF=4,点N是线段EF的中点,ME⊥AC垂足为M,则MN的最小值是2$\sqrt{3}$.
如图,菱形ABCD的边长为8,∠BAD=60°,点E在AB上运动,点F在BC上运动(E,F两点可以和菱形的顶点重合),且EF=4,点N是线段EF的中点,ME⊥AC垂足为M,则MN的最小值是2$\sqrt{3}$.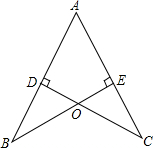 如图,AB=AC,BE⊥AC于点E,CD⊥AB于点D,BE,CD交于点O,试说明:△BDO≌△CEO.
如图,AB=AC,BE⊥AC于点E,CD⊥AB于点D,BE,CD交于点O,试说明:△BDO≌△CEO. 如图所示,Rt△ABC中,∠ACB=90°,点A坐标为(0,1),点B坐标为(0,-1),且∠ABC=30°,若反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点C,则k的值为$\frac{\sqrt{3}}{4}$.
如图所示,Rt△ABC中,∠ACB=90°,点A坐标为(0,1),点B坐标为(0,-1),且∠ABC=30°,若反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点C,则k的值为$\frac{\sqrt{3}}{4}$.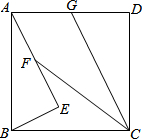 如图,E点在正方形ABCD内部,且AE⊥BE,AE=2BE,点F是线段AE的中点,连接CF,∠FCD的平分线交AD于G.
如图,E点在正方形ABCD内部,且AE⊥BE,AE=2BE,点F是线段AE的中点,连接CF,∠FCD的平分线交AD于G.