题目内容
20. 如图,在△ABC中,已知AB=AC=5,BC=6,点D、E分别在BC、AC上,且∠ADE=∠B
如图,在△ABC中,已知AB=AC=5,BC=6,点D、E分别在BC、AC上,且∠ADE=∠B(1)求证:△ABD∽△DCE;
(2)求线段AE的最小值.
分析 (1)根据两角对应相等的两个三角形相似即可判断.
(2)利用相似三角形的性质根据二次函数,利用二次函数的最值解决问题.
解答 (1)证明: ∵AB=AC,
∵AB=AC,
∴∠B=∠C,
∵∠ADE=∠B,∠ADC=∠ADE+∠EDC=∠B+∠BAD,
∴∠BAD=∠EDC,
∴△ABD∽△DCE.
(2)设AE=x,BD=y,则DC=6-y,EC=5-x
∵△ABD∽△DCE,
∴$\frac{AB}{DC}$=$\frac{BD}{EC}$,
∴$\frac{5}{6-y}$=$\frac{y}{5-x}$,
∴x=$\frac{1}{5}$(y2-6y+25)=$\frac{1}{5}$(y-3)2+$\frac{16}{5}$,
∴y=3时,x最小值=$\frac{16}{5}$.
∴AE的最小值为$\frac{16}{5}$.
点评 本题考查相似三角形的判定和性质、二次函数的性质等知识,解题的关键是构建二次函数求最值问题,系统了数形结合的思想,属于中考常考题型.

练习册系列答案
相关题目
10.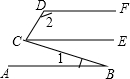 如图,AB∥CE,CE∥DF,则∠BCD等于( )
如图,AB∥CE,CE∥DF,则∠BCD等于( )
 如图,AB∥CE,CE∥DF,则∠BCD等于( )
如图,AB∥CE,CE∥DF,则∠BCD等于( )| A. | ∠2-∠1 | B. | ∠1+∠2 | C. | 180°+∠1-∠2 | D. | 180°+∠2-2∠1 |
11.下列不等式组中,无解的是( )
| A. | $\left\{\begin{array}{l}{x>-3}\\{x>2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x<-3}\\{x<2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x>-3}\\{x<2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x<-3}\\{x>2}\end{array}\right.$ |
15.新学期开学初,王刚同学对部分同学暑假在家做家务的时间进行了抽样调查(时间取整数小时),所得数据统计如下表:
(1)王刚同学抽取样本的容量是多少?
(2)请你根据表中数据补全图中的频数分布直方图;
(3)若该学校有学生1260人,那么大约有多少学生在暑假做家务的时间在40.5~100.5小时之间?
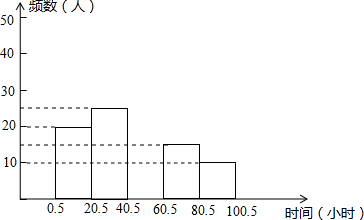
| 时间分组 | 0.5~20.5 | 20.5~40.5 | 40.5~60.5 | 60.5~80.5 | 80.5~100.5 |
| 频 数 | 20 | 25 | 30 | 15 | 10 |
(2)请你根据表中数据补全图中的频数分布直方图;
(3)若该学校有学生1260人,那么大约有多少学生在暑假做家务的时间在40.5~100.5小时之间?

 如图,已知⊙O是△ABC的外接圆,AB为直径,若PA⊥AB,PO过AC的中点M.
如图,已知⊙O是△ABC的外接圆,AB为直径,若PA⊥AB,PO过AC的中点M.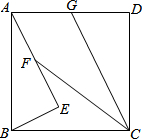 如图,E点在正方形ABCD内部,且AE⊥BE,AE=2BE,点F是线段AE的中点,连接CF,∠FCD的平分线交AD于G.
如图,E点在正方形ABCD内部,且AE⊥BE,AE=2BE,点F是线段AE的中点,连接CF,∠FCD的平分线交AD于G.