题目内容
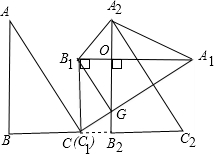
2.已知Rt△ABC,∠B=90°,AB=4,现有每个小正方形的边长为1的网格,将△ABC的点A和点B如图放置在格点上,点C在点B右侧沿着格线运动,使边BC落在格线上,且1<BC<4,将△ABC绕点C顺时针旋转90°得△A1B1C1,将△ABC向右平移五个格后得△A2B2C2,边A1C1交边A2B2于点G,在点C运动过程中.(Ⅰ)四边形A1A2B1G的面积改变(填“改变”或者“不改变”);
(Ⅱ)四边形A1A2B1G的面积=$\frac{39}{8}$(如果改变,写出四边形面积的最小值;如果不改变,写出四边形面积).

分析 根据题意,在整个图形的变化过程中,BC与四边形A1A2B1G的面积是两个变量设BC=t(1<t<4),四边形A1A2B1G的面积=s,设A1 B1 与 A2B2相交于点O,
可证明△A1 OG∽△A1 B1 C1,得OA2与OG的长即可判定四边形A1A2B1G的面积.
解答 解:如下图所示:
设BC=t(1<t<4),四边形A1A2B1G的面积=s,设 A1 B1 与A2G相交于点O
∵△ABC绕着点C旋转90°与△A1 B1 C1 重合,△ABC向右平移5个格后与△A2B2C2重合
∴A1 B1⊥B1 C${\;}_{{\;}_{1}}$,A1 B1⊥OG,
∴A1 B1∥OG
∴△A1 OG∽△A1 B1 C1
∴$\frac{{A}_{1}{B}_{1}}{{A}_{1}O}=\frac{{B}_{1}{C}_{1}}{OG}$
∴$\frac{OG}{t}=\frac{4-(5-t)}{4}$
∴OG=$\frac{{t}^{2}-t}{4}$
∴s=$\frac{1}{2}$ A1 B1•OA2+$\frac{1}{2}$ A1 B1•OG
又OA2=4-t,A1 B1=4,
∴s=$\frac{1}{2}$×4(4-t+$\frac{{t}^{2}-t}{4}$)
s=$\frac{1}{2}$t2-$\frac{5}{2}$t+8(1<t<4)
∵s=$\frac{1}{2}$t2-$\frac{5}{2}$t+8=$\frac{1}{2}$(t-$\frac{5}{2}$)2+$\frac{39}{8}$(1<t<4)
∴Smin=$\frac{39}{8}$
即:当BC的长为$\frac{5}{2}$是,四边形A1A2B1G的面积最小为$\frac{39}{8}$
点评 本题考查了图形的旋转、平移的性质,解题的关键是分析求出图象在变换过程中变化的量BC与四边形A1A2B1G的面积之间的关系.

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案| A. | 0.25×10-5 | B. | 2.5×10-6 | C. | 25×10-7 | D. | 2.5×106 |
| 销售时段 | 第一周 | 第二周 | |
| 销售数量(台) | A型 | 5 | 10 |
| B型 | 3 | 5 | |
| 销售收入(万元) | 3.98 | 7.4 | |
(2)某公司准备用不少于5万元但不超过5.2万元的金额,向该电器超市购买A,B两种型号的空调共10台,则有哪几种采购方案?
 如图是由三个相同小正方体组成的几何体的主视图,那么这个几何体可以是( )
如图是由三个相同小正方体组成的几何体的主视图,那么这个几何体可以是( )



 如图,在平面直角坐标系中,已知点A(0,2),B(4,0),C(4,3)三点.
如图,在平面直角坐标系中,已知点A(0,2),B(4,0),C(4,3)三点. 在如图所示的正方形网格中,每个小正方形的边长均为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A、C的坐标分别为(-4,5)、(-1,3).
在如图所示的正方形网格中,每个小正方形的边长均为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A、C的坐标分别为(-4,5)、(-1,3).