题目内容
11. 如图,在平面直角坐标系中,已知点A(0,2),B(4,0),C(4,3)三点.
如图,在平面直角坐标系中,已知点A(0,2),B(4,0),C(4,3)三点.(1)求△ABC的面积;
(2)如果在第二象限内有一点P(m,1),且四边形ABOP的面积是△ABC的面积的两倍;求满足条件的P点坐标.
分析 (1)由点的坐标得出BC=3,即可求出△ABC的面积;
(2)求出OA=2,OB=4,由S四边形ABOP=S△AOB+S△AOP和已知条件得出方程,解方程即可.
解答 解:(1)∵B(4,0),C(4,3),
∴BC=3,
∴S△ABC=$\frac{1}{2}$×3×4=6;
(2)∵A(0,2)(4,0),
∴OA=2,OB=4,
∴S四边形ABOP=S△AOB+S△AOP
=$\frac{1}{2}$×4×2+$\frac{1}{2}$×2(-m)=4-m,
又∵S四边形ABOP=2S△ABC=12,
∴4-m=12,
解得:m=-8,
∴P(-8,1).
点评 本题考查了坐标与图形性质、三角形和四边形面积的计算;熟练掌握坐标与图形性质,由题意得出方程是解决问题(2)的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.若一次函数$y=(m-2){x^{{m^2}-8}}$+5,y随x的增大而减小,则m的值为( )
| A. | 2或-2 | B. | 3或-3 | C. | -3 | D. | 3 |
 已知:如图,△OAB,点O为原点,点A、B的坐标分别是(2,1)、(-2,4).
已知:如图,△OAB,点O为原点,点A、B的坐标分别是(2,1)、(-2,4).
 如图,长方形ABCD中,AB=2,BC=3,点P从点B出发,沿B-C-D向终点D均匀运动,设点P走过的路程为x,△APD的面积为S,能反应S与x之间关系的图象是( )
如图,长方形ABCD中,AB=2,BC=3,点P从点B出发,沿B-C-D向终点D均匀运动,设点P走过的路程为x,△APD的面积为S,能反应S与x之间关系的图象是( )



 甲、乙两地相距300km,一辆货车和一辆轿车先后从甲地出发向乙地.如图,线段OA表示货车离开甲地的距离,y(km)与时间x(h)之间的函数关系,折线BCDE表示轿车离开甲地距离y(km)与时间x(h)之间的函数关系.请根据图象,解答下列问题:
甲、乙两地相距300km,一辆货车和一辆轿车先后从甲地出发向乙地.如图,线段OA表示货车离开甲地的距离,y(km)与时间x(h)之间的函数关系,折线BCDE表示轿车离开甲地距离y(km)与时间x(h)之间的函数关系.请根据图象,解答下列问题: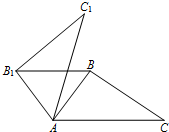 如图,在△ABC中,∠BAC=50°,将△ABC绕点A按逆时针方向旋转后得△AB1C1.当B1B∥AC时,求∠BAC1的度数.
如图,在△ABC中,∠BAC=50°,将△ABC绕点A按逆时针方向旋转后得△AB1C1.当B1B∥AC时,求∠BAC1的度数.
 如图,在平面直角坐标系上有点A(1,0),点A第一次跳动至点A1(-1,1),第四次向右跳动5个单位支至点A4(3,2),依此规律跳动下去,点A第2016次跳动至点A2016的坐标是(1009,1008).
如图,在平面直角坐标系上有点A(1,0),点A第一次跳动至点A1(-1,1),第四次向右跳动5个单位支至点A4(3,2),依此规律跳动下去,点A第2016次跳动至点A2016的坐标是(1009,1008).