题目内容
5.一组数据101,98,99,100,102的平均数$\overline{x}$=100,方差S2=2.分析 一般地设n个数据,x1,x2,…xn的平均数为$\overline{x}$,则方差S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2],据此解答即可.
解答 解:∵这组数据101,98,99,100,102的平均数$\overline{x}$=100,
∴这组数据的方差是:
S2=$\frac{1}{5}$×[(101-100)2+(98-100)2+(99-100)2+(100-100)2+(102-100)2]
=$\frac{1}{5}$×[1+4+1+0+4]
=$\frac{1}{5}$×10
=2
故答案为:2.
点评 此题主要考查了方差的定义:一般地设n个数据,x1,x2,…xn的平均数为$\overline{x}$,则方差S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
15.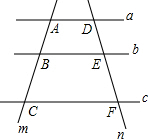 如图,直线a∥b∥c,直线m、n分别交直线a、b、c于点A、B、C、D、E、F,若AB=2,CB=DE=3,则线段EF的长为( )
如图,直线a∥b∥c,直线m、n分别交直线a、b、c于点A、B、C、D、E、F,若AB=2,CB=DE=3,则线段EF的长为( )
 如图,直线a∥b∥c,直线m、n分别交直线a、b、c于点A、B、C、D、E、F,若AB=2,CB=DE=3,则线段EF的长为( )
如图,直线a∥b∥c,直线m、n分别交直线a、b、c于点A、B、C、D、E、F,若AB=2,CB=DE=3,则线段EF的长为( )| A. | $\frac{2}{7}$ | B. | 4 | C. | $\frac{9}{2}$ | D. | 5 |
13.有一坡角为20°的滑雪道,滑雪道长为100米,坡顶到坡底的竖直高度为( )
| A. | $\frac{100}{cos20°}$ | B. | $\frac{100}{sin20°}$ | C. | 100cos20° | D. | 100sin20° |








 已知:如图,△OAB,点O为原点,点A、B的坐标分别是(2,1)、(-2,4).
已知:如图,△OAB,点O为原点,点A、B的坐标分别是(2,1)、(-2,4).