题目内容
12.解方程组:(1)$\left\{\begin{array}{l}{\frac{2x-1}{5}+\frac{3y-2}{4}=2}\\{\frac{3x+1}{5}-\frac{3y+2}{4}=0}\end{array}\right.$
(2)$\left\{\begin{array}{l}{\frac{x+y}{2}+\frac{x-y}{3}=6}\\{4(x+y)-5(x-y)=2}\end{array}\right.$.
分析 (1)方程组整理后,利用加减消元法求出解即可;
(2)方程组整理后,利用加减消元法求出解即可.
解答 解:(1)方程组整理得:$\left\{\begin{array}{l}{8x+15y=54①}\\{4x-5y=2②}\end{array}\right.$,
①+②×3得:20x=60,即x=3,
把x=3代入②得:y=2,
则方程组的解为$\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.$;
(2)方程组整理得:$\left\{\begin{array}{l}{5x+y=36①}\\{-x+9y=2②}\end{array}\right.$,
①+②×5得:46y=46,即y=1,
把y=1代入②得:x=7,
则方程组的解为$\left\{\begin{array}{l}{x=7}\\{y=1}\end{array}\right.$.
点评 此题考查了解二元一次方程组,熟练掌握运算法则是解本题的关键.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
2. 如图,△ABC中,AB=AC,BD=CE,BE=CF,若∠A=40°,则∠DEF的度数是( )
如图,△ABC中,AB=AC,BD=CE,BE=CF,若∠A=40°,则∠DEF的度数是( )
 如图,△ABC中,AB=AC,BD=CE,BE=CF,若∠A=40°,则∠DEF的度数是( )
如图,△ABC中,AB=AC,BD=CE,BE=CF,若∠A=40°,则∠DEF的度数是( )| A. | 75° | B. | 70° | C. | 65° | D. | 60° |
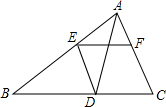 如图,AD是△ABC的角平分线,DE∥AC,EF∥BC,若AB=15,AF=4,则DE的长等于6.
如图,AD是△ABC的角平分线,DE∥AC,EF∥BC,若AB=15,AF=4,则DE的长等于6.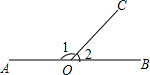 如图,点O在直线AB上,OC为射线,∠1比∠2的3倍少10°,设∠1,∠2的度数分别为x,y,那么可以列出的方程组是$\left\{\begin{array}{l}{x+y=180}\\{x=3y-10}\end{array}\right.$.
如图,点O在直线AB上,OC为射线,∠1比∠2的3倍少10°,设∠1,∠2的度数分别为x,y,那么可以列出的方程组是$\left\{\begin{array}{l}{x+y=180}\\{x=3y-10}\end{array}\right.$. 如图,反比例函数y=$\frac{k}{x}$的图象经过点A(2,2)与点B(4,m),则△AOB的面积为3.
如图,反比例函数y=$\frac{k}{x}$的图象经过点A(2,2)与点B(4,m),则△AOB的面积为3. 如图,已知AB=DC,AC=DB,AC与DB交于点M.过点C作CN∥BD,过点B作BN∥AC,CN与BN交于点N.
如图,已知AB=DC,AC=DB,AC与DB交于点M.过点C作CN∥BD,过点B作BN∥AC,CN与BN交于点N.