题目内容
1. 如图,已知AB=DC,AC=DB,AC与DB交于点M.过点C作CN∥BD,过点B作BN∥AC,CN与BN交于点N.
如图,已知AB=DC,AC=DB,AC与DB交于点M.过点C作CN∥BD,过点B作BN∥AC,CN与BN交于点N.(1)求证:△ABC≌△DCB;
(2)求证:四边形BNCM是菱形.
分析 (1)利用SSS定理可直接判定△ABC≌△DCB;
(2)首先根据CN∥BD、BN∥AC,可判定四边形BNCM是平行四边形,再根据△ABC≌△DCB可得∠1=∠2,进而可得BM=CM,根据邻边相等的平行四边形是菱形可得结论.
解答  解:(1)∵在△ABC和△DCB中$\left\{\begin{array}{l}{AB=DC}\\{AC=DB}\\{CB=BC}\end{array}\right.$,
解:(1)∵在△ABC和△DCB中$\left\{\begin{array}{l}{AB=DC}\\{AC=DB}\\{CB=BC}\end{array}\right.$,
∴△ABC≌△DCB(SSS);
(2)∵CN∥BD、BN∥AC,
∴四边形BNCM是平行四边形,
∵△ABC≌△DCB,
∴∠1=∠2,
∴BM=CM,
∴四边形BNCM是菱形.
点评 此题主要考查了全等三角形的判定和性质,以及菱形的判定,关键是掌握一组邻边相等的平行四边形是菱形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.将二次函数y=x2-2x化为y=(x-h)2+k的形式,结果为( )
| A. | y-(x-1)2 | B. | y=(x-1)2-1 | C. | y=(x+1)2+1 | D. | y=(x-1)2+1 |
6.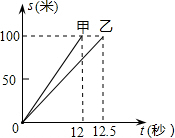 甲、乙两人在一次赛跑中,路程s与时间t的关系如图所示.下列关于此次赛跑说法正确的是( )
甲、乙两人在一次赛跑中,路程s与时间t的关系如图所示.下列关于此次赛跑说法正确的是( )
 甲、乙两人在一次赛跑中,路程s与时间t的关系如图所示.下列关于此次赛跑说法正确的是( )
甲、乙两人在一次赛跑中,路程s与时间t的关系如图所示.下列关于此次赛跑说法正确的是( )| A. | 乙比甲跑的路程多 | B. | 这是一次100米赛跑 | ||
| C. | 甲乙同时到达终点 | D. | 甲的速度为8m/s |
13.为了解学校九年级学生某次知识问卷的得分情况,小红随机调查了50名九年级同学,结果如表:
则这50名同学问卷得分的众数和中位数分别是( )
| 知识问卷得分 (单位:分) | 65 | 70 | 75 | 80 | 85 |
| 人数 | 1 | 15 | 15 | 16 | 3 |
| A. | 75,75 | B. | 75,80 | C. | 80,75 | D. | 80,85 |