题目内容
5. 如图,已知Rt△ABC中,∠BCA=90°,CD是斜边上的中线,BC=12,AC=5,那么
如图,已知Rt△ABC中,∠BCA=90°,CD是斜边上的中线,BC=12,AC=5,那么CD=$\frac{13}{2}$.
分析 根据勾股定理求出AB的长,根据在直角三角形中,斜边上的中线等于斜边的一半解答.
解答 解:∵∠BCA=90°,BC=12,AC=5,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=13,
∵CD是斜边上的中线,
∴CD=$\frac{1}{2}$AB=$\frac{13}{2}$,
故答案为:$\frac{13}{2}$.
点评 本题考查的是直角三角形的性质,在直角三角形中,斜边上的中线等于斜边的一半.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.若方程x2-3x-1=0的两根为x1、x2,则x1x2的值为( )
| A. | -3 | B. | 3 | C. | -1 | D. | 1 |
16.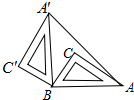 如图,Rt△ABC中,∠C=90°,AC=8,BC=6,△ABC绕着点B逆时针旋转90°到△A′B′C′的位置,AA′的长为( )
如图,Rt△ABC中,∠C=90°,AC=8,BC=6,△ABC绕着点B逆时针旋转90°到△A′B′C′的位置,AA′的长为( )
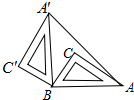 如图,Rt△ABC中,∠C=90°,AC=8,BC=6,△ABC绕着点B逆时针旋转90°到△A′B′C′的位置,AA′的长为( )
如图,Rt△ABC中,∠C=90°,AC=8,BC=6,△ABC绕着点B逆时针旋转90°到△A′B′C′的位置,AA′的长为( )| A. | 10$\sqrt{2}$ | B. | 10 | C. | 20 | D. | 5$\sqrt{2}$ |
10.下列结论中错误的是( )
| A. | 若a=b,则ac-3=bc-3 | B. | 若a=b,则$\frac{a}{c^2+1}$=$\frac{b}{c^2+1}$ | ||
| C. | 若x=3,则x2=3x | D. | 若ax=bx,则a=b |
17.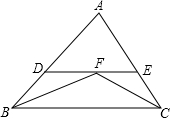 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点F,过点F作DE∥BC,交AB于点D,交AC于点E.若BD+CE=2013,则线段DE的长为( )
如图,在△ABC中,∠ABC和∠ACB的平分线相交于点F,过点F作DE∥BC,交AB于点D,交AC于点E.若BD+CE=2013,则线段DE的长为( )
 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点F,过点F作DE∥BC,交AB于点D,交AC于点E.若BD+CE=2013,则线段DE的长为( )
如图,在△ABC中,∠ABC和∠ACB的平分线相交于点F,过点F作DE∥BC,交AB于点D,交AC于点E.若BD+CE=2013,则线段DE的长为( )| A. | 2014 | B. | 2011 | C. | 2012 | D. | 2013 |
14.若|a|=8,则a的值是( )
| A. | -8 | B. | 8 | C. | ±8 | D. | ±$\frac{1}{8}$ |
 如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A沿AB向点B以1cm/s的速度移动,同时点Q从点B沿BC向点C以2cm/s的速度移动,当其中一点到达终点时,另一点也随之停止.
如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A沿AB向点B以1cm/s的速度移动,同时点Q从点B沿BC向点C以2cm/s的速度移动,当其中一点到达终点时,另一点也随之停止.