题目内容
16.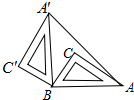 如图,Rt△ABC中,∠C=90°,AC=8,BC=6,△ABC绕着点B逆时针旋转90°到△A′B′C′的位置,AA′的长为( )
如图,Rt△ABC中,∠C=90°,AC=8,BC=6,△ABC绕着点B逆时针旋转90°到△A′B′C′的位置,AA′的长为( )| A. | 10$\sqrt{2}$ | B. | 10 | C. | 20 | D. | 5$\sqrt{2}$ |
分析 由勾股定理得出AB=10,再根据旋转的性质可得∠ABA′=90°,AB=A′B=10,继而可得AA′的长.
解答 解:∵∠C=90°,AC=8,BC=6,
∴AB=10,
∵△ABC绕着点B逆时针旋转90°到△A′B′C′的位置,
∴∠ABA′=90°,AB=A′B=10,
∴AA′=$\sqrt{A{B}^{2}+A′{B}^{2}}$=$\sqrt{1{0}^{2}+1{0}^{2}}$=10$\sqrt{2}$,
故选:A.
点评 本题主要考查勾股定理和旋转的性质,根据旋转的性质得出对应边相等是解题的关键.

练习册系列答案
相关题目
4.下列几组数据中,能作为直角三角形三边长的是( )
| A. | 2,3,4 | B. | 1,2,3 | C. | 1,$\frac{1}{2}$,$\frac{1}{3}$ | D. | 7,24,25 |
11.下列运算中,结果错误的是( )
| A. | 3a2+a2=4a2 | B. | x3•x=x4 | C. | (x2)3=x6 | D. | x6÷x2=x3 |
1.在某一年期间,我国内地吸引外来直接投资累计为4880亿美元,用科学记数法表示正确的是________亿美元.( )
| A. | 4.880×102 | B. | 4.880×103 | C. | 0.4880×104 | D. | 48.80×102 |

 如图,已知Rt△ABC中,∠BCA=90°,CD是斜边上的中线,BC=12,AC=5,那么
如图,已知Rt△ABC中,∠BCA=90°,CD是斜边上的中线,BC=12,AC=5,那么 (1)将抛物线y1=2x2向右平移2个单位,得到抛物线y2的图象,求y2的解析式;
(1)将抛物线y1=2x2向右平移2个单位,得到抛物线y2的图象,求y2的解析式;