Question

17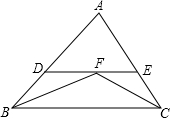．如图，在△ABC中，∠ABC和∠ACB的平分线相交于点F，过点F作DE∥BC，交AB于点D，交AC于点E．若BD+CE=2013，则线段DE的长为（　　）

• A． 2014
• B． 2011
• C． 2012
• D． 2013

Answer 1

分析 根据△ABC中，∠ABC和∠ACB的平分线相交于点F．求证∠DBF=∠FBC，∠ECF=∠BCF，再利用两直线平行内错角相等，求证出∠DFB=∠DBF，∠CFE=∠BCF，即BD=DF，FE=CE，然后利用等量代换即可求出线段DE的长．

解答 解：∵∠ABC和∠ACB的平分线相交于点F，
∴∠DBF=∠FBC，∠ECF=∠BCF，
∵DE∥BC，交AB于点D，交AC于点E．
∴∠DFB=∠DBF，∠CFE=∠ECF，
∴BD=DF，FE=CE，
∴DE=DF+CE=2013．
故选D．

点评 本题主要考查了学生对等腰三角形的判定与性质和平行线段性质的理解和掌握，此题难度不大，是一道基础题．