题目内容
19.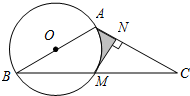 如图,在△ABC中,以AB为直径的⊙O交于BC点M,MN⊥AC于点N.
如图,在△ABC中,以AB为直径的⊙O交于BC点M,MN⊥AC于点N.(1)求证:MN是⊙O的切线;
(2)若∠BAC=120°,AB=2,求图中阴影部分的面积.
分析 (1)先判定OM⊥MN,再说明点M在圆上即可,
(2)圆中阴影部分面积的计算,用割补法求解.
解答 证明:(1)如图,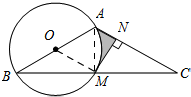
连接OM.
∵OM=OB,
∴∠B=∠OMB.
∵AB=AC,
∴∠B=∠C.
∴∠OMB=∠C.
∴OM∥AC.
∵MN⊥AC,
∴OM⊥MN.
∵点M在⊙O上,
∴MN是⊙O的切线.
(2)如图,
连接AM.
∵AB为直径,点M在⊙O上,
∴∠AMB=90°.
∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°.
∴∠AOM=60°.
又∵在Rt△AMC中,MN⊥AC于点N,
∴∠AMN=30°.
∴AN=AM•sin∠AMN=AC•sin30°•sin30°=$\frac{1}{2}$
∴MN=AM•cos∠AMN=AC•sin30°•cos30°=$\frac{\sqrt{3}}{2}$
∴S 梯形ANMO=$\frac{(AN+OM)MN}{2}$=$\frac{3\sqrt{3}}{3}$,
S 扇形OAM=$\frac{60π×1}{360}$=$\frac{π}{6}$,
∴S 阴影=$\frac{9\sqrt{3}-4π}{24}$.
点评 此题是切线的判定题,主要考查了切线的判定定理,用割补法求阴影部分的面积,解本题的关键是阴影部分面积的计算.

练习册系列答案
相关题目
17. 如图,△ABC内接于⊙O,连接OA,OB,∠C=40°,则∠OBA的度数是( )
如图,△ABC内接于⊙O,连接OA,OB,∠C=40°,则∠OBA的度数是( )
 如图,△ABC内接于⊙O,连接OA,OB,∠C=40°,则∠OBA的度数是( )
如图,△ABC内接于⊙O,连接OA,OB,∠C=40°,则∠OBA的度数是( )| A. | 60° | B. | 50° | C. | 45° | D. | 40° |
7.在下列以线段a,b,c的长为三边的三角形中,不能构成直角三角形的是( )
| A. | a=5,b=13,c=12 | B. | a=11,b=12,c=15 | C. | a:b:c=3:4:5 | D. | a=b=1,c=$\sqrt{2}$ |
14.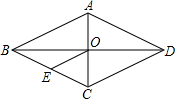 已知:如图,菱形ABCD中,对角线AC与BD相交于点O,OE∥AB交BC于点E,AD=6cm,则OE的长为( )
已知:如图,菱形ABCD中,对角线AC与BD相交于点O,OE∥AB交BC于点E,AD=6cm,则OE的长为( )
 已知:如图,菱形ABCD中,对角线AC与BD相交于点O,OE∥AB交BC于点E,AD=6cm,则OE的长为( )
已知:如图,菱形ABCD中,对角线AC与BD相交于点O,OE∥AB交BC于点E,AD=6cm,则OE的长为( )| A. | 6cm | B. | 4cm | C. | 3cm | D. | 2cm |