题目内容
7.在下列以线段a,b,c的长为三边的三角形中,不能构成直角三角形的是( )| A. | a=5,b=13,c=12 | B. | a=11,b=12,c=15 | C. | a:b:c=3:4:5 | D. | a=b=1,c=$\sqrt{2}$ |
分析 根据勾股定理的逆定理,验证四个选项中数据是否满足“较小两边平方的和等于最大边的平方”,由此即可得出结论.
解答 解:A、52+122=169,132=169,
∵169=169,
∴a=5,b=13,c=12能构成直角三角形;
B、112+122=265,152=225,
∵265≠225,
∴a=11,b=12,c=15不能构成直角三角形;
C、(3x)2+(4x)2=25x2,(5x)2=25x2,
∵25x2=25x2,
∴a:b:c=3:4:5能构成直角三角形;
D、12+12=2,($\sqrt{2}$)2=2,
∵2=2,
∴a=b=1,c=$\sqrt{2}$能构成直角三角形.
故选B.
点评 本题考查了勾股定理的逆定理,解题的关键是根据勾股定理的逆定理验证四个选项.本题属于基础题,难度不大,解决该题型题目时,套入数据验证“较小两边平方的和是否等于最大边的平方”是关键.

练习册系列答案
相关题目
5.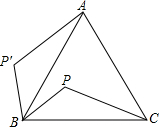 如图,P是等边三角形△ABC内的一点,连接PB、PC.若将△PBC绕点B旋转到△P′BA,则∠PBP′的度数是( )
如图,P是等边三角形△ABC内的一点,连接PB、PC.若将△PBC绕点B旋转到△P′BA,则∠PBP′的度数是( )
 如图,P是等边三角形△ABC内的一点,连接PB、PC.若将△PBC绕点B旋转到△P′BA,则∠PBP′的度数是( )
如图,P是等边三角形△ABC内的一点,连接PB、PC.若将△PBC绕点B旋转到△P′BA,则∠PBP′的度数是( )| A. | 45° | B. | 60° | C. | 90° | D. | 120° |
16.下列各式,计算正确的是( )
| A. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | B. | 3$\sqrt{3}-\sqrt{3}$=3 | C. | 2$\sqrt{5}×3\sqrt{5}=6\sqrt{5}$ | D. | ($\sqrt{8}-\sqrt{6}$)÷$\sqrt{2}$=2-$\sqrt{3}$ |
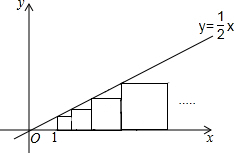 如图,在直线y=$\frac{1}{2}$x的下方依次作小正方形,每个小正方形的一个顶点都在直线y=$\frac{1}{2}$x上,若最小的正方形左边顶点的横坐标是1,则从左到右第10个小正方形的边长是$\frac{19683}{1024}$.
如图,在直线y=$\frac{1}{2}$x的下方依次作小正方形,每个小正方形的一个顶点都在直线y=$\frac{1}{2}$x上,若最小的正方形左边顶点的横坐标是1,则从左到右第10个小正方形的边长是$\frac{19683}{1024}$.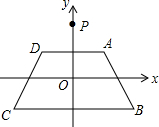 如图,在平面直角坐标系xOy中,等腰梯形ABCD的顶点坐标为A(1,1),B(2,-1),C(-2,-1),D(-1,1)现将y轴上一点P(0,2)绕点A旋转180°得到点P1,点P1绕点B旋转180°得点P2,点P2绕点C旋转180°得点P3,点P3绕点D旋转180°得点P4,又将点P4绕点A旋转180°得点P5,又将点P5绕点B旋转180°得点P6…,按此方法操作依次得到P1,P2,…,则点P2016的坐标是(2016,2).
如图,在平面直角坐标系xOy中,等腰梯形ABCD的顶点坐标为A(1,1),B(2,-1),C(-2,-1),D(-1,1)现将y轴上一点P(0,2)绕点A旋转180°得到点P1,点P1绕点B旋转180°得点P2,点P2绕点C旋转180°得点P3,点P3绕点D旋转180°得点P4,又将点P4绕点A旋转180°得点P5,又将点P5绕点B旋转180°得点P6…,按此方法操作依次得到P1,P2,…,则点P2016的坐标是(2016,2).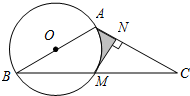 如图,在△ABC中,以AB为直径的⊙O交于BC点M,MN⊥AC于点N.
如图,在△ABC中,以AB为直径的⊙O交于BC点M,MN⊥AC于点N.