题目内容
14.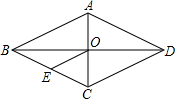 已知:如图,菱形ABCD中,对角线AC与BD相交于点O,OE∥AB交BC于点E,AD=6cm,则OE的长为( )
已知:如图,菱形ABCD中,对角线AC与BD相交于点O,OE∥AB交BC于点E,AD=6cm,则OE的长为( )| A. | 6cm | B. | 4cm | C. | 3cm | D. | 2cm |
分析 首先根据菱形的性质可得AO=CO,AB=AD=6cm,再根据三角形中位线定义和性质可得BA=2OE,进而得到答案.
解答 解:∵四边形ABCD是菱形,
∴AO=CO,AB=AD=6cm,
∵E为CB的中点,
∴OE是△ABC的中位线,
∴BA=2OE,
∴OE=3cm.
故选C.
点评 此题主要考查了菱形的性质,以及三角形中位线性质,解题关键是掌握菱形的四边相等这一重要性质.

练习册系列答案
相关题目
12.运用乘法公式计算(a+3)(a-3)的结果是( )
| A. | a2-6a+9 | B. | a2-3a+9 | C. | a2-9 | D. | a2-6a-9 |
9. 实数a在数轴上的位置如图所示,则化简|1-a|+$\sqrt{(a-2)^{2}}$的结果是( )
实数a在数轴上的位置如图所示,则化简|1-a|+$\sqrt{(a-2)^{2}}$的结果是( )
 实数a在数轴上的位置如图所示,则化简|1-a|+$\sqrt{(a-2)^{2}}$的结果是( )
实数a在数轴上的位置如图所示,则化简|1-a|+$\sqrt{(a-2)^{2}}$的结果是( )| A. | -1 | B. | 1 | C. | 2a-3 | D. | 3-2a |
3. 如图,AB∥CD,CD∥EF,∠1=115°,则∠2的度数是( )
如图,AB∥CD,CD∥EF,∠1=115°,则∠2的度数是( )
 如图,AB∥CD,CD∥EF,∠1=115°,则∠2的度数是( )
如图,AB∥CD,CD∥EF,∠1=115°,则∠2的度数是( )| A. | 115° | B. | 85° | C. | 75° | D. | 65° |
4.下列说法正确的是( )
| A. | -64的立方根是4 | B. | 9的平方根是±3 | ||
| C. | 4的算术平方根是16 | D. | 0.1的立方根是0.001 |
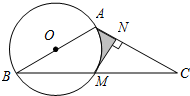 如图,在△ABC中,以AB为直径的⊙O交于BC点M,MN⊥AC于点N.
如图,在△ABC中,以AB为直径的⊙O交于BC点M,MN⊥AC于点N.