题目内容
9.等腰梯形的上、下两底及高之比为1:4:2,它们的腰比高长1cm,求梯形的面积.分析 作AE⊥BC于E,DF⊥BC于F,则EF=AD,BE=CF=$\frac{1}{2}$(BC-AD),设AD=xcm,则BC=4xcm,DF=2xcm,CF=$\frac{3}{2}$x,CD=(2x+1)cm,由勾股定理得出方程,解方程求出AD,得出BC、DF的长,即可求出梯形的面积.
解答 解:如图所示: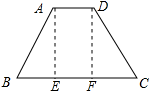
作AE⊥BC于E,DF⊥BC于F,如图所示:
则EF=AD,BE=CF=$\frac{1}{2}$(BC-AD),
∵等腰梯形的上、下两底及高之比为1:4:2,
∴设AD=xcm,则BC=4xcm,DF=2xcm,CF=$\frac{3}{2}$x,CD=(2x+1)cm,
由勾股定理得:CF2+DF2=CD2,
即($\frac{3}{2}$x)2+(2x)2=(2x+1)2,
解得:x=2,或x=-$\frac{2}{9}$,
∴AD=2cm,BC=8cm,DF=4cm,
∴梯形ABCD的面积=$\frac{1}{2}$(AD+BC)×DF=$\frac{1}{2}$(2+8)×4=20(cm2).
点评 本题考查了等腰梯形的性质、勾股定理、梯形面积的计算;熟练掌握等腰梯形的性质,运用勾股定理得出方程是解决问题的关键.

练习册系列答案
相关题目
19.下列长度的三条线段中能组成一个三角形的是( )
| A. | 1、2、3 | B. | 2、4、8 | C. | 10、8、9 | D. | 9、3、5 |
17.下面的命题是真命题的有( )
| A. | 有一组邻边相等的平行四边形是正方形 | |
| B. | 有一组邻边相等且有一角为直角的四边形为正方形 | |
| C. | 正方形是一组对边相等的矩形 | |
| D. | 正方形是有一个角为直角的菱形 |
 如图所示,则x的取值范围是-3<x≤2.
如图所示,则x的取值范围是-3<x≤2.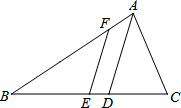 如图,在△ABC中,∠C=2∠B,AD平分∠BAC交BC于点D,点E为BC中点,EF∥AD交AB于点F.若BF=4AF,CD=$\frac{12}{5}$,则AC=$\frac{18}{5}$.
如图,在△ABC中,∠C=2∠B,AD平分∠BAC交BC于点D,点E为BC中点,EF∥AD交AB于点F.若BF=4AF,CD=$\frac{12}{5}$,则AC=$\frac{18}{5}$.