题目内容
如图,∠1=65°,∠2=65°,∠3=115°.试说明:DE∥BC,DF∥AB.根据图形,完成下面的推理:
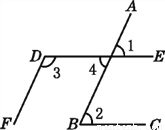
因为∠1=65°,∠2=65°,
所以∠1=∠2.
所以______________∥ ( ).
因为AB与DE相交,
所以∠1=∠4( ).
所以∠4=65°.
又因为∠3=115°,
所以∠3+∠4=180°.
所以 ∥ ( ).
DE;BC;同位角相等,两直线平行;对顶角相等;DF;AB;同旁内角互补,两直线平行
【解析】试题分析：由同位角相等，两直线平行可得DE∥BC，由对顶角相等可得∠4=65°，再由同旁内角互补，两直线平行可得DF∥AB.
试题解析：因为∠1=65°，∠2=65°，
所以∠1=∠2.
所以DE∥BC (同位角相等，两直线平行).
因为AB与DE相交，
所以∠1=∠...
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
（8分）如果A=2x2+3kx﹣2x﹣1，B=﹣x2+kx﹣1，且3A+6B的值与x的取值无关，求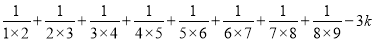
的值．
【解析】试题分析：把A、B代入3A+6B，由3A+6B的值与x的取值无关可求出k的值；把k代入代数式进行计算即可．注意利用 将式子化简．
【解析】
3A+6B=3（2x2+3kx﹣2x﹣1）+6（﹣x2+kx﹣1）
=6x 2+9xk-6x-3-6x 2+6xk-6
=15xk-6x-9
=（15k-6）x-9 ,
∵3A+6B的值与x的取值无关，
∴15k=... 如图，若A是有理数a在数轴上对应的点，则关于a，－a，1的大小关系表示正确的是( )
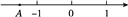
A. a＜1＜－a B. a＜－a＜1 C. 1＜－a＜a D. －a＜a＜1
A
【解析】试题分析：a和﹣a互为相反数，首先表示﹣a的位置，然后再根据当数轴方向朝右时，右边的数总比左边的数大进行比较．
【解析】
如图所示：
由数轴可得：a＜1＜﹣a，
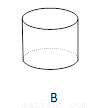
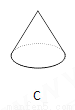
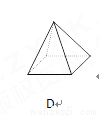
故选：A． 下面立体图形，从正面、左面、上面观察都不可能看到长方形的是( )
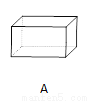
C
【解析】试题分析：A、主视图为长方形，左视图为长方形，俯视图为长方形，故本选项错误；
B、主视图为长方形，左视图为长方形，俯视图为圆，故本选项错误；
C、主视图为等腰三角形，左视图为等腰三角形，俯视图为圆，从正面、左面、上面观察都不可能看到长方形，故本选项正确；
D、主视图为三角形，左视图为三角形，俯视图为有对角线的矩形，故本选项错误．
故选：C． 如图,工人师傅在工程施工中需在同一平面内弯制一个变形管道ABCD,使其拐角∠ABC=150°,∠BCD=30°,则( )
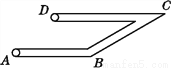
A. AB∥BC B. BC∥CD C. AB∥DC D. AB与CD相交
C
【解析】试题分析：根据同旁内角互补，两直线平行即可求解
本题解析：由∠ABC=150°，∠BCD=30°，得∠ABC+∠BCD=180°，
所以AB∥CD.故选C. 在我们常见的英文字母中,也存在着同位角、内错角、同旁内角,在下面几个字母中,含有内错角最少的字母是( )
A. 
B. 
C. 
D. 
C
【解析】根据内错角的定义可知H中含有2对内错角，M中含有2对内错角；N中含有1对，A中含有2对内错角.
故选：C. 如图，△ABC中，D、E在AB上，且D、E分别是AC、BC的垂直平分线上一点．
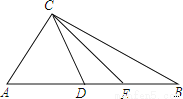
（1）若△CDE的周长为4，求AB的长；
（2）若∠ACB=100°，求∠DCE的度数；
（3）若∠ACB=a（90°＜a＜180°），则∠DCE=___________.
（1）4；（2）20°；（3）2α-180°.
【解析】试题分析：（1）根据线段的垂直平分线的性质得到DC=DA，EC=EB，根据三角形的周长公式计算即可；
（2）根据三角形内角和定理求出∠A+∠B的度数，根据等腰三角形的性质求出∠DCA+∠ECB，根据题意计算即可；
（3）根据（2）的方法解答．
试题解析：（1）∵D、E分别是AC、BC的垂直平分线上一点，
∴DC=... 如图,已知△ABE≌△ACD,∠1=∠2,∠B=∠C,指出其他的对应边和对应角.
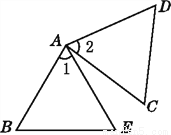
见解析
【解析】试题分析：先根据△ABE≌△ACD，可以确定点A的对应点是A，点B的对应点是C，点D的对应点是E，然后根据对应顶点，结合图形即可找出对应边和对应角.
试题解析：∵△ABE≌△ACD，∠1=∠2，∠B=∠C，
∴点A的对应点是A，点B的对应点是C，点E的对应点是D，
∴∠BAE与∠CAD是对应角，AB与AC，BE与CD，AD与AE是对应边.