题目内容
在我们常见的英文字母中,也存在着同位角、内错角、同旁内角,在下面几个字母中,含有内错角最少的字母是( )
A. 
B. 
C. 
D. 
C
【解析】根据内错角的定义可知H中含有2对内错角，M中含有2对内错角；N中含有1对，A中含有2对内错角.
故选：C.
练习册系列答案
相关题目
星期天小明和同学们去郊外爬山，得到如下数据：
爬坡长度x(米) | 40 | 80 | 120 | 160 | 200 | 240 |
爬坡时间t(分) | 2 | 5 | 9 | 14 | 20 | 30 |
(1)当爬到120米时，所用时间是多少？
(2)爬坡速度随时间是怎样变化的？
(1)9分钟； (2)爬坡速度随时间的增加而减小． 【解析】试题分析：(1)观察表格信息可知爬坡120m时,所需时间为9分钟 (2)计算爬坡相同的距离所用的时间，即可得出结论. 试题解析：(1)观察表格信息可知爬坡120m时,所需时间为9分钟 (2)由图表可知爬坡长度分别为40m和80m时,所用时间分别为2分钟和5分钟 故此时爬坡每增加10m时,所需时间为分钟 ...如图，若开始输入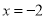
，则最后输出的结果是______．
-10
【解析】∵(-2) ×3-(-2)=-6+2=-4>-5，
(-4) ×3-(-2)=-12+2=-10<-5.
∴最后输出的结果是-10. 如图,∠1=65°,∠2=65°,∠3=115°.试说明:DE∥BC,DF∥AB.根据图形,完成下面的推理:
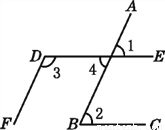
因为∠1=65°,∠2=65°,
所以∠1=∠2.
所以______________∥ ( ).
因为AB与DE相交,
所以∠1=∠4( ).
所以∠4=65°.
又因为∠3=115°,
所以∠3+∠4=180°.
所以 ∥ ( ).
DE;BC;同位角相等,两直线平行;对顶角相等;DF;AB;同旁内角互补,两直线平行
【解析】试题分析：由同位角相等，两直线平行可得DE∥BC，由对顶角相等可得∠4=65°，再由同旁内角互补，两直线平行可得DF∥AB.
试题解析：因为∠1=65°，∠2=65°，
所以∠1=∠2.
所以DE∥BC (同位角相等，两直线平行).
因为AB与DE相交，
所以∠1=∠... 如图,在四边形ABCD中,连接AC,BD,若要使AB∥CD,则需要添加的条件是( )
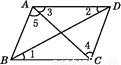
A. ∠1=∠2 B. ∠2=∠3 C. ∠3=∠4 D. ∠4=∠5
D
【解析】A、当∠1=∠2时, AD∥BC ,故此选项错误;
B、当∠2=∠3时,无法得到AB∥CD,故此选项错误;
C、当∠3=∠4时,无法得到AB∥CD,故此选项错误;
D、当∠4=∠5时, AB∥CD,故此选项正确.
故选D. 如图，已知∠1=∠2，AC平分∠DAB，试说明AB//DC；
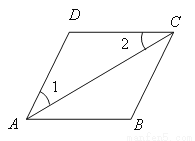
证明见解析
【解析】试题分析：根据角平分线的性质可得,再加上条件,可得,再根据内错角相等两直线平行可得.
证明：∵ AC平分∠DBA（ 已知 ）
∴ ∠1=∠BAC （ 角平分线定义）
又∵∠1=∠2 （ 已知 ）
∴ ∠BAC =∠2 （ 等量代换 ）
∴ AB//DC ( 内错角相等，两直线平行 ) 如图,在四边形ABCD中,连接AC,BD,若要使AB∥CD,则需要添加的条件是( )
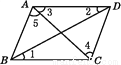
A. ∠1=∠2 B. ∠2=∠3 C. ∠3=∠4 D. ∠4=∠5
D
【解析】A、当∠1=∠2时, AD∥BC ,故此选项错误;
B、当∠2=∠3时,无法得到AB∥CD,故此选项错误;
C、当∠3=∠4时,无法得到AB∥CD,故此选项错误;
D、当∠4=∠5时, AB∥CD,故此选项正确.
故选D. 如图,AB=DC,∠A=∠D.试说明:∠ABC=∠DCB.
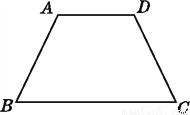
说明见解析.
【解析】试题分析：连接AC、BD，利用“边角边”证明△ABD和△DCA全等，根据全等三角形对应边相等可得AC=BD，再利用“边边边”证明△ABC和△DCB全等，根据全等三角形对应角相等证明即可．
试题解析：证明：如图，连接AC、BD，
在△ABD和△DCA中，
，
∴△ABD≌△DCA（SAS），
∴AC=BD，
在△ABC和△DCB中，
... 如图，在Rt△ABC中，∠ACB=90°，∠B=30°，AD平分∠CAB．
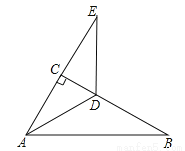
（1）求∠CAD的度数；
（2）延长AC至E，使CE=AC，求证：DA=DE．
30°；见解析．
【解析】试题分析：根据∠ACB和∠B的度数得出∠CAB的度数，根据角平分线的性质得出∠CAD的度数；根据∠ACD+∠ECD=180°，∠ACD=90°得出∠ACD=∠ECD=90°，证明△ACD和△ECD全等，从而得出结论．
试题解析：（1）∵在Rt△ABC中，∠ACB=90°，∠B=30°， ∴∠CAB=60°．
又∵AD平分∠CAB， ∴∠CAD=∠CAB=...