题目内容
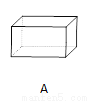
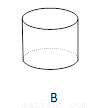
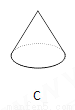
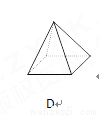
下面立体图形,从正面、左面、上面观察都不可能看到长方形的是( )
 C
【解析】试题分析:A、主视图为长方形,左视图为长方形,俯视图为长方形,故本选项错误;
B、主视图为长方形,左视图为长方形,俯视图为圆,故本选项错误;
C、主视图为等腰三角形,左视图为等腰三角形,俯视图为圆,从正面、左面、上面观察都不可能看到长方形,故本选项正确;
D、主视图为三角形,左视图为三角形,俯视图为有对角线的矩形,故本选项错误.
故选:C.
C
【解析】试题分析:A、主视图为长方形,左视图为长方形,俯视图为长方形,故本选项错误;
B、主视图为长方形,左视图为长方形,俯视图为圆,故本选项错误;
C、主视图为等腰三角形,左视图为等腰三角形,俯视图为圆,从正面、左面、上面观察都不可能看到长方形,故本选项正确;
D、主视图为三角形,左视图为三角形,俯视图为有对角线的矩形,故本选项错误.
故选:C.
练习册系列答案
相关题目
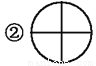
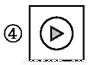
下列图标是由我们熟悉的一些基本数学图形组成的,其中是轴对称图形的是__________.(填序号)

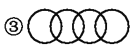
 ①②③④
【解析】①是轴对称图形,②是轴对称图形,③是轴对称图形,④是轴对称图形,
故答案为:①②③④.
①②③④
【解析】①是轴对称图形,②是轴对称图形,③是轴对称图形,④是轴对称图形,
故答案为:①②③④. 如图,若开始输入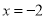 ,则最后输出的结果是______.
,则最后输出的结果是______.

 -10
【解析】∵(-2) ×3-(-2)=-6+2=-4>-5,
(-4) ×3-(-2)=-12+2=-10<-5.
∴最后输出的结果是-10.
-10
【解析】∵(-2) ×3-(-2)=-6+2=-4>-5,
(-4) ×3-(-2)=-12+2=-10<-5.
∴最后输出的结果是-10. 若 是关于
是关于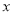 的方程
的方程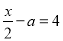 的解,则
的解,则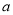 的值为( )
的值为( )
A. -6 B. 2 C. 16 D. -2
 D
【解析】把代入方程得:2-a=4,解得:a=-2,
故选D.
D
【解析】把代入方程得:2-a=4,解得:a=-2,
故选D. 如图,∠1=65°,∠2=65°,∠3=115°.试说明:DE∥BC,DF∥AB.根据图形,完成下面的推理:
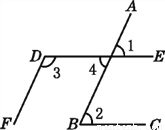
因为∠1=65°,∠2=65°,
所以∠1=∠2.
所以______________∥ ( ).
因为AB与DE相交,
所以∠1=∠4( ).
所以∠4=65°.
又因为∠3=115°,
所以∠3+∠4=180°.
所以 ∥ ( ).
 DE;BC;同位角相等,两直线平行;对顶角相等;DF;AB;同旁内角互补,两直线平行
【解析】试题分析:由同位角相等,两直线平行可得DE∥BC,由对顶角相等可得∠4=65°,再由同旁内角互补,两直线平行可得DF∥AB.
试题解析:因为∠1=65°,∠2=65°,
所以∠1=∠2.
所以DE∥BC (同位角相等,两直线平行).
因为AB与DE相交,
所以∠1=∠...
DE;BC;同位角相等,两直线平行;对顶角相等;DF;AB;同旁内角互补,两直线平行
【解析】试题分析:由同位角相等,两直线平行可得DE∥BC,由对顶角相等可得∠4=65°,再由同旁内角互补,两直线平行可得DF∥AB.
试题解析:因为∠1=65°,∠2=65°,
所以∠1=∠2.
所以DE∥BC (同位角相等,两直线平行).
因为AB与DE相交,
所以∠1=∠... 如图,在四边形ABCD中,连接AC,BD,若要使AB∥CD,则需要添加的条件是( )
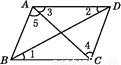
A. ∠1=∠2 B. ∠2=∠3 C. ∠3=∠4 D. ∠4=∠5
 D
【解析】A、当∠1=∠2时, AD∥BC ,故此选项错误;
B、当∠2=∠3时,无法得到AB∥CD,故此选项错误;
C、当∠3=∠4时,无法得到AB∥CD,故此选项错误;
D、当∠4=∠5时, AB∥CD,故此选项正确.
故选D.
D
【解析】A、当∠1=∠2时, AD∥BC ,故此选项错误;
B、当∠2=∠3时,无法得到AB∥CD,故此选项错误;
C、当∠3=∠4时,无法得到AB∥CD,故此选项错误;
D、当∠4=∠5时, AB∥CD,故此选项正确.
故选D. 如图,在四边形ABCD中,连接AC,BD,若要使AB∥CD,则需要添加的条件是( )
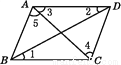
A. ∠1=∠2 B. ∠2=∠3 C. ∠3=∠4 D. ∠4=∠5
 D
【解析】A、当∠1=∠2时, AD∥BC ,故此选项错误;
B、当∠2=∠3时,无法得到AB∥CD,故此选项错误;
C、当∠3=∠4时,无法得到AB∥CD,故此选项错误;
D、当∠4=∠5时, AB∥CD,故此选项正确.
故选D.
D
【解析】A、当∠1=∠2时, AD∥BC ,故此选项错误;
B、当∠2=∠3时,无法得到AB∥CD,故此选项错误;
C、当∠3=∠4时,无法得到AB∥CD,故此选项错误;
D、当∠4=∠5时, AB∥CD,故此选项正确.
故选D. 如图,已知△ABE≌△ACD,且AB=AC.
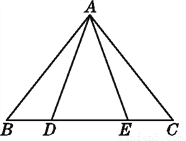
(1)说明△ABE经过怎样的变换后可与△ACD重合.
(2)∠BAD与∠CAE有何关系?请说明理由.
(3)BD与CE相等吗?为什么?
 (1)见解析;(2)∠BAD=∠CAE;(3)相等
【解析】试题分析:(1)由几何变换的类型说明即可,
(2)由三角形全等的性质求解即可,
(3)由三角形全等的性质求解即可.
试题解析: (1)△ABE先水平翻转,再平移即可与△ACD重合;
(2)∠BAD=∠CAE.
∵△ABE≌△ACD,
∴∠BAE=∠CAD,
∴∠BAE?∠DAE=∠CAD?∠...
(1)见解析;(2)∠BAD=∠CAE;(3)相等
【解析】试题分析:(1)由几何变换的类型说明即可,
(2)由三角形全等的性质求解即可,
(3)由三角形全等的性质求解即可.
试题解析: (1)△ABE先水平翻转,再平移即可与△ACD重合;
(2)∠BAD=∠CAE.
∵△ABE≌△ACD,
∴∠BAE=∠CAD,
∴∠BAE?∠DAE=∠CAD?∠...