题目内容
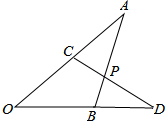 如图,已知AC=BD,∠A=∠D,AB、CD交于点P,求证:点P到OA、OD的距离相等.
如图,已知AC=BD,∠A=∠D,AB、CD交于点P,求证:点P到OA、OD的距离相等.考点:全等三角形的判定与性质,角平分线的性质
专题:证明题
分析:作PE⊥AC,PF⊥BD,易证△ACP≌△DBP,可得PA=PD,即可证明△APE≌△DPF,可得PE=PF,即可解题.
解答:证明:作PE⊥AC,PF⊥BD,
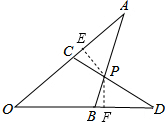
在△ACP和△DBP中,
,
∴△ACP≌△DBP(AAS),
∴PA=PD,
在△APE和△DPF中,
,
∴△APE≌△DPF(AAS),
∴PE=PF.

在△ACP和△DBP中,
|
∴△ACP≌△DBP(AAS),
∴PA=PD,
在△APE和△DPF中,
|
∴△APE≌△DPF(AAS),
∴PE=PF.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△ACP≌△DBP和△APE≌△DPF是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
 已知:如图,△ABC内接于圆,AB=AC,D为延长线上一点,AD交圆于E.求证:AB2=AD•AE.
已知:如图,△ABC内接于圆,AB=AC,D为延长线上一点,AD交圆于E.求证:AB2=AD•AE.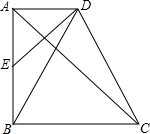 如图,在四边形ABCD中,AD∥BC,∠BAD=90°,E为AB的中点,AC是ED的垂直平分线
如图,在四边形ABCD中,AD∥BC,∠BAD=90°,E为AB的中点,AC是ED的垂直平分线 如图,教室里挂的时钟,时针、分针、秒针均按时匀速转动,分别用OB、OA、OC来表示.
如图,教室里挂的时钟,时针、分针、秒针均按时匀速转动,分别用OB、OA、OC来表示.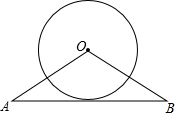 已知,OA=OB=5cm,AB=8cm,⊙O的直径为6cm.求证:AB与⊙O相切.
已知,OA=OB=5cm,AB=8cm,⊙O的直径为6cm.求证:AB与⊙O相切. 如图,东西方向的海岸线上有A、B两码头,相距100(
如图,东西方向的海岸线上有A、B两码头,相距100( 如图,在等腰直角三角形ABC中,∠ACB=90°,D为斜边AB上一点,连接CD,过点A、B分别向CD作垂线,垂足分别为点F、E,试判断AF、BE与EF之间的数量关系,并证明你的结论.
如图,在等腰直角三角形ABC中,∠ACB=90°,D为斜边AB上一点,连接CD,过点A、B分别向CD作垂线,垂足分别为点F、E,试判断AF、BE与EF之间的数量关系,并证明你的结论. 如图,在平面直角坐标系xOy中,点A(0,5),点B(6,5).
如图,在平面直角坐标系xOy中,点A(0,5),点B(6,5).