题目内容
如图，东西方向的海岸线上有A、B两码头，相距100（| 3 |
| 3 |
考点：解直角三角形的应用-方向角问题
专题：
分析：根据题意设AC=xkm，故BC=100（
-1）-xkm，利用锐角三角函数关系表示出KC的长，再求出x的值即可得出答案．
| 3 |
解答：解：由题意可得：∠KAC=60°，∠KBC=75°，
则设AC=xkm，故BC=100（
-1）-xkm，
则tan60°=
=
=
，
故KC=
xkm，则tan75°=
=
=2+
，
解得：x=50，
故KC=50
（km）．
答：船K距海岸线AB的距离为50
km．
则设AC=xkm，故BC=100（
| 3 |
则tan60°=
| KC |
| AC |
| KC |
| x |
| 3 |
故KC=
| 3 |
| KC |
| BC |
| ||
100(
|
| 3 |
解得：x=50，
故KC=50
| 3 |
答：船K距海岸线AB的距离为50
| 3 |
点评：此题主要考查了解直角三角形的应用，根据题意表示出KC的长是解题关键．
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
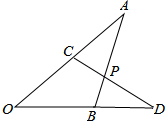如图，已知AC=BD，∠A=∠D，AB、CD交于点P，求证：点P到OA、OD的距离相等．
如图，已知四边形ABCD中，AD∥BC，∠C=90°，∠B=30°，以D为圆心，DC为半径的圆交AD于点．若CE的长为2π，BC=8+4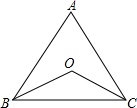
如图，在△ABC中，∠ABC，∠ACB的角平分线相交于点O，
如图，在△ABC中，AB=AC，AD是△ABC的角平分线，DE⊥AB，DF⊥AC，垂足分别为E、F，则下列四个结论：