题目内容
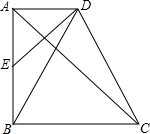 如图,在四边形ABCD中,AD∥BC,∠BAD=90°,E为AB的中点,AC是ED的垂直平分线
如图,在四边形ABCD中,AD∥BC,∠BAD=90°,E为AB的中点,AC是ED的垂直平分线(1)求证:AB=BC;
(2)求证:∠DBC=∠DCB.
考点:全等三角形的判定与性质,线段垂直平分线的性质,等腰直角三角形
专题:证明题
分析:(1)如图,作辅助线;证明AD=AE,CD=CE;DF=AB=2λ,CF=BC-λ;由勾股定理证明BC=2λ,即可解决问题.
(2)证明BF=CF,得到DF垂直平分BC,即可解决问题.
(2)证明BF=CF,得到DF垂直平分BC,即可解决问题.
解答:证明: (1)如图,连接CE;过点D作DF⊥BC;
(1)如图,连接CE;过点D作DF⊥BC;
∵AC是ED的垂直平分线,
∴AD=AE,CD=CE;
∵E为AB的中点,
∴BE=AE=AD(设为λ);
∵AD∥BC,∠BAD=90°,
∴四边形ABFD是矩形,
∴DF=AB=2λ,CF=BC-λ;
由勾股定理得:
CE2=λ2+BC2,CD2=(2λ)2+(BC-λ)2,
∴λ2+BC2=4λ2+(BC-λ)2,
解得:BC=2λ,
∴AB=BC.
(2)∵BC=2λ,BF=λ,
∴BF=CF,即DF垂直平分BC,
∴BD=CD,
∴∠DBC=∠DCB.
 (1)如图,连接CE;过点D作DF⊥BC;
(1)如图,连接CE;过点D作DF⊥BC;∵AC是ED的垂直平分线,
∴AD=AE,CD=CE;
∵E为AB的中点,
∴BE=AE=AD(设为λ);
∵AD∥BC,∠BAD=90°,
∴四边形ABFD是矩形,
∴DF=AB=2λ,CF=BC-λ;
由勾股定理得:
CE2=λ2+BC2,CD2=(2λ)2+(BC-λ)2,
∴λ2+BC2=4λ2+(BC-λ)2,
解得:BC=2λ,
∴AB=BC.
(2)∵BC=2λ,BF=λ,
∴BF=CF,即DF垂直平分BC,
∴BD=CD,
∴∠DBC=∠DCB.
点评:该题主要考查了线段垂直平分线的性质、勾股定理及其应用等几何知识点的应用问题;解题的关键是作辅助线,构造直角三角形.

练习册系列答案
相关题目
 如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于D,若∠D=45°,则∠PCA=( )
如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于D,若∠D=45°,则∠PCA=( )| A、50° | B、57.5° |
| C、60° | D、67.5° |
 如图,⊙O的直径AB与弦CD相交于E,
如图,⊙O的直径AB与弦CD相交于E,
 已知二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=1,下列结论中:
已知二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=1,下列结论中: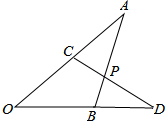 如图,已知AC=BD,∠A=∠D,AB、CD交于点P,求证:点P到OA、OD的距离相等.
如图,已知AC=BD,∠A=∠D,AB、CD交于点P,求证:点P到OA、OD的距离相等.